この連載記事は、半導体の格子欠陥の解析評価に興味を持つ人を対象に連載記事として書いています。前回から引き続き、4H-SiC中のショックレー型部分転位と、ショックレー型積層欠陥のコントラストについて説明します。 “その(7)”では、積層欠陥の変位ベクトルRの説明をしました。今回は、積層欠陥の変位ベクトルRを使って、積層欠陥のコントラスト出現のルール2πg・R ≠2nπ (n= 0, ±1, ±2, ±3, ….) について説明します。2π g・R ≠2nπの時に積層欠陥のコントラストが現れますが、2π g・R = 2nπの時には積層欠陥のコントラストは現れません。消えています。前回にも書きましたが、このルールは転位のコントラスト出現とは別のルールです。積層欠陥のトポグラフ像を観察する際の、必要最低限の話を書きます。また積層欠陥が複数枚存在する場合について説明します。なるべく理解しやすいように、天下り的な解説をします。
1枚のショックレー型積層欠陥のコントラストルール
前回の“その(7)”の図7-1ではR=1/3[0110]の積層欠陥を観察した像ですが、g=1108では積層欠陥部に薄いグレーのコントラストが表れていますが、g= 1128、g=1128では積層欠陥のコントラストは表れていません。g=1108の場合を考えます。2πg・Rの式に実際の逆格子ベクトルの長さ、変位ベクトルの長さと、変位ベクトルと逆格子ベクトルとのなす角度のcosの値を代入すると 2πg・R = -2π/3 とななります。この場合、積層欠陥のコントラストは出現します。一方、g= 1128、g=1128では 2πg・R = ±2π となります。この場合、積層欠陥のコントラストは現れません。天下り式に説明すると、2π g・R ≠2nπの時に積層欠陥のコントラストが現れますが、2π g・R = 2nπの時には積層欠陥のコントラストは現れません。連載の“その(7)で説明したように変位ベクトルRは、積層欠陥の下側の結晶の上側に対する変位を表しています。この判定式2πg・Rは回折を起こしている結晶面が変位ベクトルRによってどのように変位するのかを表現しています。図8-1(a)は周期的な(1108)面がどのようにRベクトルによってシフトするかを模式的に示しています。
周期的な(1108)面の1周期の面間隔を位相で表現すると、-2π/3の結晶格子面の位相シフトが積層欠陥を挟んだ上側結晶と下側結晶との間で発生していることを示しています。そして位相のずれた2つの結晶が歪み無く接続して接着していています。上と下の2つの結晶の結晶面(1108)面は並行ですが積層欠陥部で格子面の周期構造の不連続な位相がずれています。X線回折や、電子線回折ではこの部分で面白い事が発生します。これにより、積層欠陥が無い場所の回折強度とは異なる回折強度になります。この面白いことが積層欠陥部で回折強度差を生じさせ、コントラストを生成させていて、X線トポグラフ像や透過型電子顕微鏡像で積層欠陥が独特のコントラストを発生させています。
図8-1(a)のような変位を伴った状態では、X線回折や電子線回折ではどういう面白い効果が発生するかは、話が少し専門的になるので、ここではこれ以上は説明しませんが、透過型電子顕微鏡法に関する教科書や、X線トポグラフ法に関する教科書には、必ず説明が載っている話です。X線トポグラフ法や透過型電子顕微鏡を使って結晶性の材料を対象に仕事をしている研究者は知っている話です。
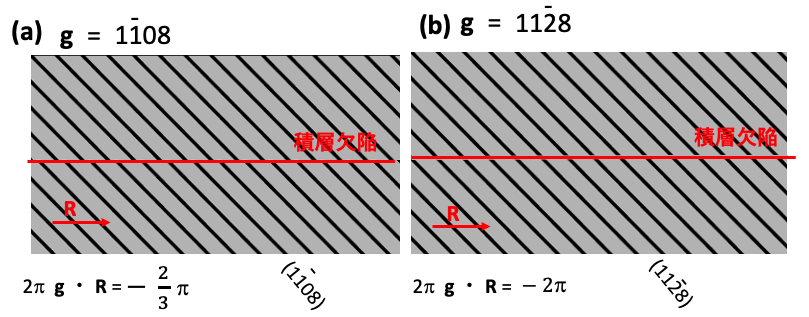
一方、図8-1(b)のg= 1128では、周期的な(1128)面に対して変位ベクトルRは-2πの位相シフトを下側の結晶で発生させます。この例について考えてみます。2π g・R = -2π の場合,
g・R =cosα ( 1/d ) | R | = ± 1 になります。
αはgベクトルとRベクトルの間の角度、Rはショックレー型積層欠陥の変位ベクトル、dは(1128)の面間隔です。回折を起こしている(1128)面の面間隔方向に、積層欠陥の変位ベクトルRを投影した場合、(1128)面の面間隔の1周期分の位相のシフトを意味しています。面間隔の1周期分のシフトでは (1128)面に不連続は発生しません。(1128)面の1周期分の結晶格子のシフトは積層欠陥の縁にある部分転位の場所で発生しますので、その格子歪みによる部分転位のコントラストは発生しますが、(1128)面の周期構造の1周期分の位相シフトでは、シフトしていないことと同じなので積層欠陥のコントラストは出現しません。
(1128)面のみを見た場合、積層欠陥の部分では上の結晶と下の結晶の(1128)面は連続的に繋がっています。つまり(1128)面で回折の効果を利用して積層欠陥を観察すると積層欠陥は見なかった事になっています。このことにより、g= 1128では、ショックレー型積層欠陥のコントラストが現れません。これが、2πg・R ≠2nπ (n= 0, ±1, ±2, ±3, ….)の場合は積層欠陥のコントラストが観察されます、という判定式の意味です。g=1108反射では積層欠陥のコントラストが観察されましたが、g=1108の場合、2πg・R = -2π/3なので、積層欠陥のコントラストルールを考えるとg=1108反射の3倍の長さの逆格子ベクトル3g反射で観察すると、積層欠陥のコントラストは消失するはずです。
放射光を使ったX線トポグラフ法ではありませんが、実験室のX線トポグラフ装置で撮影したショックレー型積層欠陥の観察例が、A. Tanaka, et al., J. Appl. Phys. ; 119 095711 (2016)の Fig. 5に示されています。このFigureでは、4H-SiCのC面側で作製されたP-i-N構造で発生した順方向特性劣化現象により発生したショックレー型積層欠陥の観察例です。観察する際に用いたgベクトルを変えることによってショックレー型積層欠陥のコントラストが現れたり、消失したりする例が示されています。ショックレー型積層欠陥のコントラストに興味がある方は、この論文をご覧ください。
積層欠陥のコントラストルールは転位のコントラストのルールとは異なることを説明しました。ショックレー型積層欠陥が放射光X線トポグラフ像で表れた場合、色々な反射で積層欠陥を撮影し、“その(7)”で述べたショックレー型部分転位の特徴や、今回説明したショックレー型積層欠陥のコントラストルールを併用すると、観察された積層欠陥がどういう変位ベクトルを持っているのか、観察されたショックレー型部分転位がどういうバーガース・ベクトルを持っているかは解析が可能だと思います。
以上の説明は、ショックレー型積層欠陥が1枚の場合ですが、4H-SiCではショックレー型積層欠陥が多数枚近接して存在していることがあり、さらに複雑で面白いことが起こります。それについて、次に説明します。







コメントを残す