この微小歪みの方向は、 ξ x b などと示すことができます。この微小な歪みとも同時にgベクトルが直交しないとコントラストは消失しません。刃状転位の場合、g・b = 0の条件とともに、スカラー3重積g・(ξ xb ) = 0がコントラスト消失の条件として加わります。ξ x bのベクトルの長さにはこの場合意味はなく、これは単に方向のみに意味を持たせていてまた逆向きかどうかもこの場合に限り意味を持たせないことにします。g・(ξ x b ) /⎹ ξ x b⎹ としておいても良いと思いますが、話を簡単にするためg・(ξ x b )=0としておきます。これをまとめると、らせん転位では g・b = 0のとき、コントラストが消失、刃状転位では g・b = 0 なおかつ g・(ξ x b )=0のとき、コントラストが消失となります。らせん転位では常に、g・(ξ x b )=0 なので、刃状転位のコントラスト消滅の条件は、らせん転位のコントラスト消滅の条件もカバーしているとも考えられます。一般に転位は蛇行したりしています。蛇行部分は混合転位部で、混合転位の歪みは、らせん転位の歪み成分と、刃状転位の歪み成分により成り立っているので、混合転位のコントラスト消滅の条件は、g・b = 0 なおかつ g・(ξ x b )=0となります。転位のコントラストが消失するgベクトルを探せば観察している転位のバーガース・ベクトルが求められるということになります。しかしながら、放射光ベルク・バレットX線トポグラフ法では面白いことが起こっていて、もっと簡単にバーガース・ベクトルを求めることができます。以降に基底面転位のコントラストについて述べ、簡単にバーガース・ベクトルを求める方法を説明します。
基底面らせん転位のコントラスト
図4-3(a)、 (b)、(c) はそれぞれ、g=1128、 g=1128、g=1108の回折条件で撮影された4H-SiCのベアウエハ表面の放射光ベルクバレットX線トポグラフ像です。我々の実験は、大部分、0.15nmの近くの波長のX線で行っています。
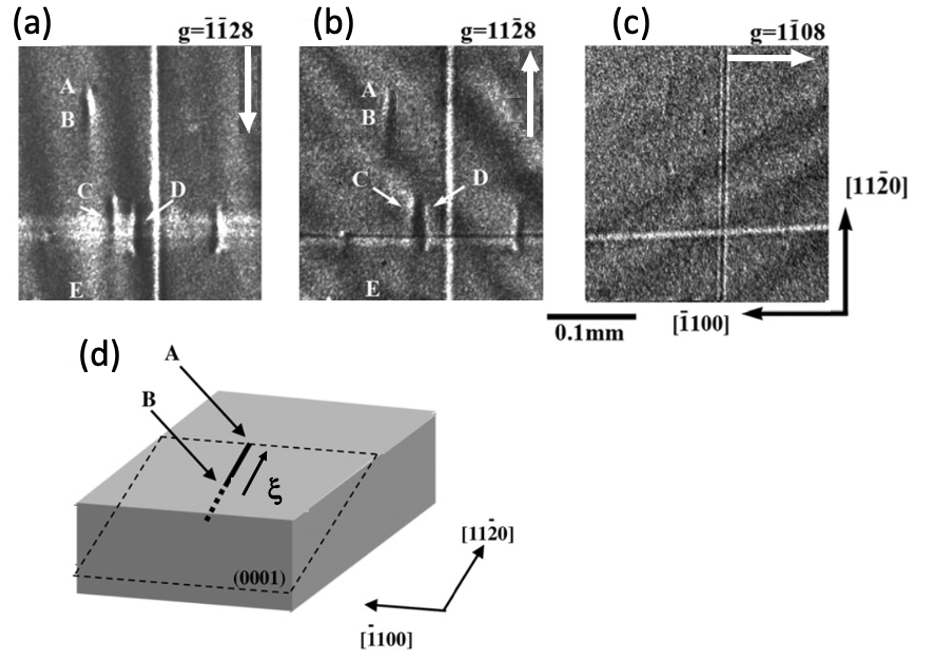
(a)、(b)、(c)の図中の白矢印はウエハ表面上にgべクトルを投影したときのgべクトルの向きを表現しています。縦方向、横方向の長い線は、ウエハ表面に描かれていたエッチングパターンなのでこれは転位ではありませんが、この線のおかげで(a),(b),(c)とも同じ位置の像であることはわかると思います。 図4-3(a), (b) ではABで示した短い線状のコントラストや、C、 D、と表示した短い線状のコントラストが観察されますが、図4-3(c) ではこれらのコントラストは消失しています。このことよりAB、C、Dは基底面らせん転位で、そのバーガース・ベクトルはg=1108に垂直方向、つまりb=±1/3[1120]であろうことがすぐに推察されます。転位の向きもバーガース・ベクトルと平行または反平行になっています。基底面らせん転位ABはBの方向へ行くのに従ってコントラストは弱くなっています。この試料では基底面とウエハ表面は8度の角度をなしていて、Aの位置でこの転位が表面で終端していて、B方向ではより深い方に基底面が沈んで行くことがわかります。図4-3(d)のように配置されていることが推察されます。図4-3で観察されている転位はいずれも、b=±1/3[1120]の基底面らせん転位ですが、2種類の異なるコントラストのものが観察されています。
g=1128の回折条件では、基底面らせん転位ABは左側が黒、右側が白ですが、基底面らせん転位Dは左側が白、右側が黒です。別ものと考えられると推察されます。一方、g=1128の回折条件では、基底面らせん転位ABは左側が白、右側が黒ですが、基底面らせん転位Dは左側が黒、右側が白となって逆転しています。これらの白黒のコントラストは、基底面らせん転位の周りの剪断歪みの符号に対応していることが推察されます。これらの像は原子核乾板で撮影したものを光学顕微鏡で撮影していて、黒い部分ではX線の強度は強くなっていることを示していて、白い部分はX線の強度は弱くなっているところを示しています。放射光ベルク・バレットX線トポグラフ法では、基底面らせん転位は転位に沿って白黒の非対称コントラストを示すことがわかります。また、白黒コントラストのつき方から、b=1/3[1120]なのかb=1/3[1120]なのかの区別もつきそうなことがわかります。どちらかが、b=1/3[1120]の基底面らせん転位、もう片方がb=1/3[1120] の基底面らせん転位です。図4-3から分かることは以上です。次回では基底面転位のループの観察結果とその解析について紹介します。基底面転位ループのコントラストを見ると、色々と新しいことが理解できます。







コメントを残す