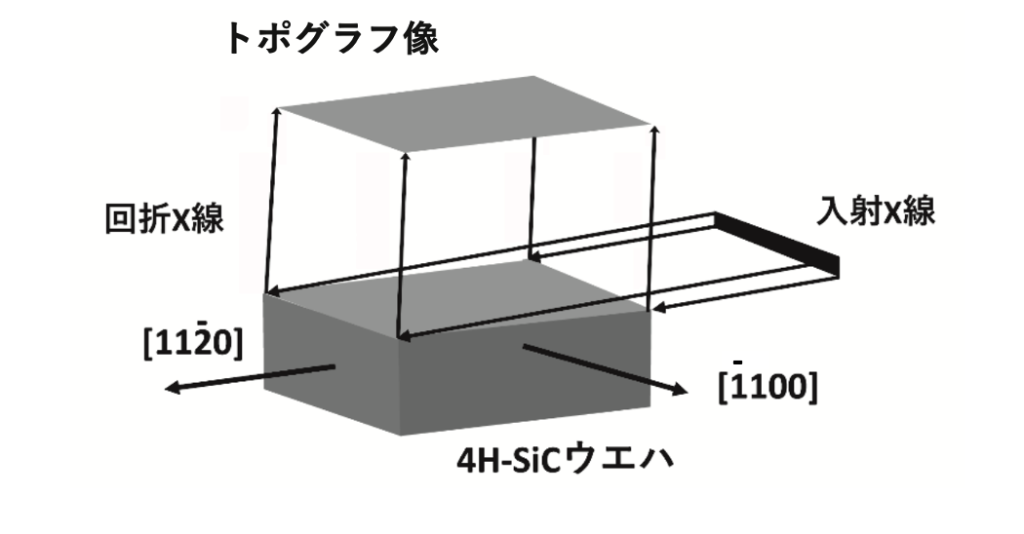
図4-2(a)は4H-SiCの放射光ベルク・バレットX線トポグラフ法による観察を行う時の試料の配置の一例です。ベルク・バレット法では、入射X線は結晶表面に浅い角度で入射させ、入射した表面と同じ表面から出てくる回折X線による像を撮影します。この手法では、結晶の表面と入射X線とがなす角度を変えるとX線の侵入深さを変えることができます。このことによって、ごく表面直下のみの転位や、ある程度の深さの位置にある転位など、観察する深さの範囲を調整することができます。エピ層中の転位組織のみを観察するとか、エピ層と基板のある程度の深さのみ、パワーデバイス部中の転位組織のみを観察する等、観察する深さを調整することができるので便利です。なぜそれが可能なのか?と聞かれたことがあるので、簡単に説明します。図4-2(b)は入射X線が浅い角度で結晶中に侵入している状態を模式的に示しています。
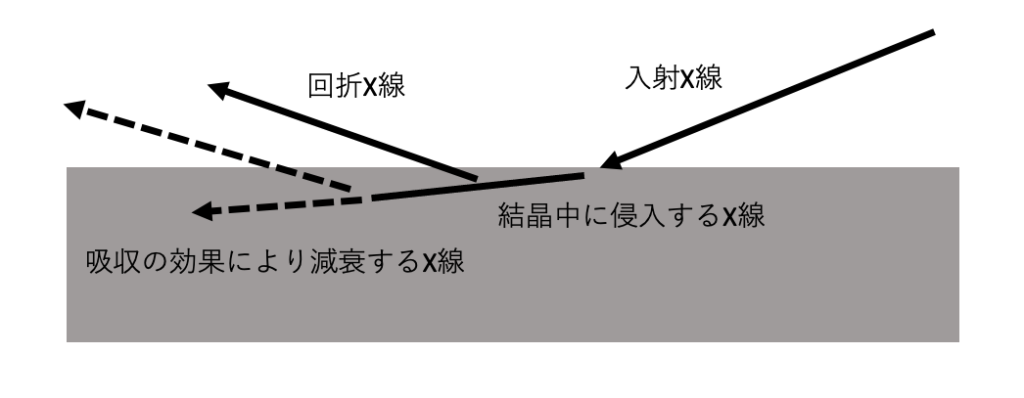
結晶中に入射したX線は、非弾性散乱を伴ってexp関数的に強度の減衰を起こしながら侵入します。このため結晶の深いところへ到達する前にほぼ消えてしまいます。目的とする深さまでのトポグラフ像を観察するには、観察を行う反射にブラッグ条件を合わせておいて、なおかつ入射X線と結晶表面との角度を変えて調節します。そのためには入射X線の波長を連続的に変えることが必要です。放射光を用いるとX線の波長を連続的に変化させることが可能です。X線の波長を少しずつ変えながら、ウエハの表面と入射X線のなす角を少しずつ調整すると、侵入深さを調整することができます。実験室のX線トポグラフ装置を利用すると、連続的に波長を変化させることができないので、X線の侵入深さを自由に変えることができません、とは言うものの観察するブラッグ反射を選べばある程度の調節は可能です。
観察されている像の実際の深さはどうやって調べるのか?との質問を何度か受けています。どの程度の深さまでのトポグラフ像が観察されるかを実際に調べるには、基底面とウエハ表面とが例えば4度の角度をもつ4度オフ基板を観察し、表面で終端している基底面転位がどの程度の長さ(深さ)まで観察されているかを見れば、観察可能な深さを知ることができます。この時に原子核乾板やX線フィルムなどの記録媒体をウエハ表面と平行にセットしておけば、ウエハ表面でのX線の屈折の効果による像の歪みは避けることはできます。一般に4H-SiCのウエハにはセンチメートル単位の長範囲の緩やかでうねったような結晶格子の歪みがビルトインされています。ウエハ中にそれなりの密度で転位が存在しているので、これらの長範囲の格子歪みの存在は仕方のないことです。この長範囲の歪みは局所的にわずかに像を拡大させたり縮小させたり歪ませたりするので、長さの計測データーはある程度の精度しかない大雑把な値と考えておいた方が安全です。
転位が観察される回折条件
X線トポグラフ法では、とある反射で回折を起こさせなければ転位などの格子欠陥を観察することはできませんが、いずれのブラッグ反射を利用しても転位の像が観察されるのかというとそうではありません。回折を起こしている結晶面は逆格子ベクトルgで示すことができます。逆格子ベクトルの向きは、その結晶面と垂直方向の向きを持っていて、その長さは結晶面の面間隔の逆数です。逆格子ベクトルの単位は、長さの単位の逆数です。図4-1の場合、回折を起こしている面のgベクトルの向きは図の上方向に向いています。転位の周囲の格子歪みを示しているバーガース・ベクトルの向きも上むきなので、この場合、回折を起こしている面間隔は転位の周囲で変化していて、コントラストを発生させています。
次に、図4-1の回折条件で、らせん転位の場合を想定してみます。らせん転位が紙面に垂直に存在していると、らせん転位のバーガース・ベクトルは、図4-1の紙面に対して垂直方向を向いています。結晶格子は紙面に垂直な方向に変位し、回折を起こしている結晶面の間隔dに変化を与えません。つまり、図4-1の回折状態では、紙面に垂直ならせん転位が存在していても、コントラストは発生せず、見ることはできません。
らせん転位の場合、転位の向きξに結晶格子の剪断歪みが存在していますが, その方向はbと同じです。らせん転位はg・b = 0のとき、コントラストが消失し、見ることができません。回折を起こす反射を変えて、色々な反射でらせん転位を観察し、コントラストが消失すれば、バーガース・ベクトルはそのgベクトルに垂直方向であることがわかります。このような現象を利用して、転位を記述する重要なパラメターのバーガース・ベクトルを求めることができます。刃状転位の場合を考えてみます。刃状転位の場合、転位の周辺にバーガース・ベクトルと同じ向きに回折を起こしている結晶面の膨張と収縮を伴う歪みが存在するので、g・b = 0になるようなg を選べば、刃状転位のコントラストは消失するように思えますが、これのみでは転位コントラスト消失の条件として十分な条件ではありません。その(3)で、Cコア刃状転位、Siコア刃状転位の図を示しました。図3-2に示しているように刃状転位の場合、バーガース・ベクトルの方向以外にも格子の歪みを伴っています。その刃状転位特有の微小な格子歪みは、図3-2の上下方向に存在していて、図3-2(a)では上凸、図3-2(b)では下凸の緩やかな格子歪みを伴っています。







コメントを残す