3-2-2. (B)式を用いた3段研磨最適条件
次に、Pn = Xn (vn)の関数は(B)式の関数だと想定して最適研磨条件を考察してみます。
(B)式はPn = Xn (vn) = dn vn 1/2 と設定されています。この時、v3 = Y3(F) = (F/a3 )2になります。
3-2-1.と同様のやり方で得られる3段研磨の局所的最適研磨時間TLはv1の関数として、
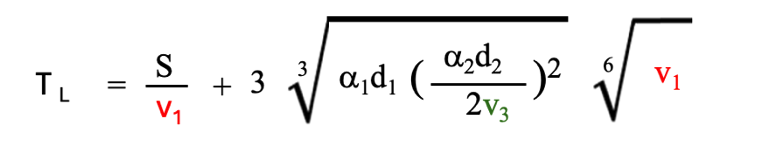
(3-8)
で示されます。このTLも最小値をとるv1を求めることができます。3-2-1.と同様のやり方でv1,t1,v2,t2,v3,t3を求めることができます。
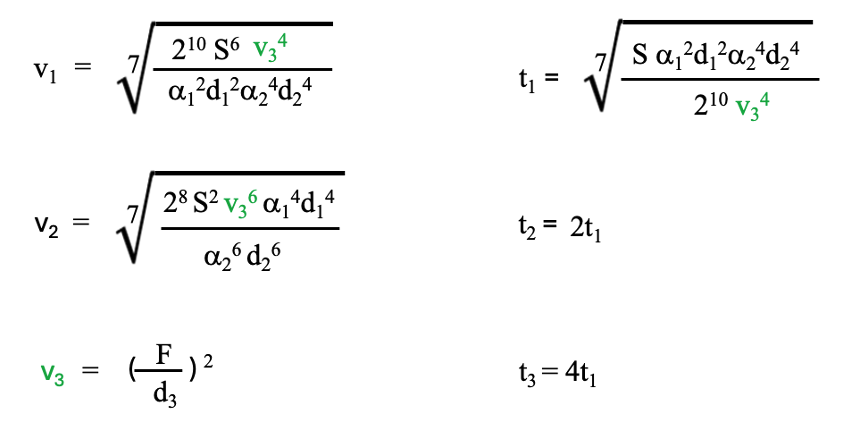
(3-9)
(3-4)式の場合と同様に、各段の研磨速度は一意的に指定されてしまいます。そしてこの研磨速度の条件で、t2=2t1, t3=4t1と、研磨時間が指定されます。この条件で最適研磨が達成されます。全研磨時間は、以下のように一意的に決定されます。

(3-10)
2段目の研磨は1段目の研磨より研磨速度は遅い場合を想定しています。v1>>v2となる条件を設定すると以下の条件が設定されます。
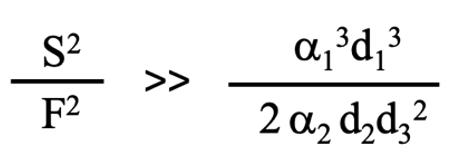
これは実際の値を代入しないとこの条件は成立するかどうかは不明ですが、通常はS>>Fの時にこの条件は満たされていることとします。もしこの条件が満たされないときは、v2>v1なので1段目の研磨を省略した2段研磨が優位になってくると考えられます。
次にv2>>v3という条件をつけると、
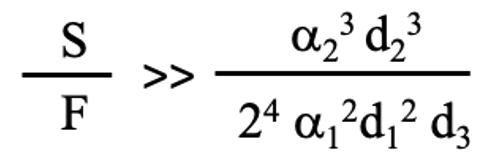
という条件が出てきます。これも、S>>Fの時に成立します。3段研磨が優位な条件とは、上記の2つの不等式を満たすSとFが設定されている時です。






