3-1. はじめに
この記事はSiCウエハの加工・研磨に興味を持つ人を対象に書いています。SiCウエハの切断・研磨工程の統合化された最適条件について考察しています。前回の連載の(2)では、2段研磨の最適条件について考察しました。今回は3段の研磨について同様の考察を行います。

図3-1はSiCウエハ研磨を3段に分けて研磨する場合のモデル図です。粗い研磨を行う前の状態として、ウエハ表面には切断時に導入された大きな表面凹凸と厚い加工変質層が存在しています。粗研磨ではこれらの大きな表面凹凸と厚い加工変質層を取り除くことを目的として、比較的大きな粒径の砥粒を用いて、速い研磨速度で研磨します。粗研磨の後、ウエハの洗浄を行い、粗研磨時に発生した研磨屑などを取り除きます。2番目の中研磨で、さらに表面を平坦にしながら、粗研磨によって導入された加工変質層を取り除きます。3段目の仕上げ研磨では、さらに表面を平坦にしながら、2番目の中研磨で導入された加工変質層を取り除きます。最後の仕上げ研磨では、加工変質層の厚みを最少の厚みにします。この3段研磨最適条件について、2段研磨の場合と同様に考察します。
3-2. 3段研磨最適条件の考察
3段研磨の全研磨時間は、洗浄時間を除いて
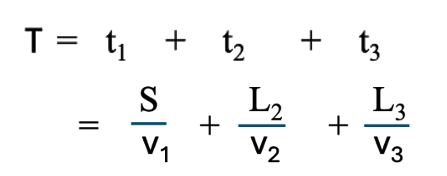
(3-1)
で示されます。ここで、t1,t2,t3は3段のそれぞれの研磨時間、v1,v2,v3は3段のそれぞれの研磨速度、Sは粗研磨で削り落とす目標とする厚みで
S = α0 P0と設定します。
P0は単結晶から輪切り切断プロセスによって導入された加工変質層の厚み、α0は安全係数です。(3-1)式のL2は2段目の研磨で削り落とす目標の厚みで、これは1段目の研磨で導入された加工変質層の厚みP1に安全係数α1をかけた値で、L2 = α1P1です。ここでP1 = X1(v1)と設定します。P1はv1の何らかの現象論的関数とします。L2 = α1 X1(v1) と示すことができます。L3も同様にL3 = α2 X2(v2) と示すことができます。
そして最終の仕上げ研磨の目標の加工変質層の厚みFはF = P3 = X3(v3)ですが、逆の関数、v3= Y3(F)を定義しているので、目標とする最終仕上げの状態Fを設定するとv3は一意的に固定されてしまいます。
(3-1)式は、
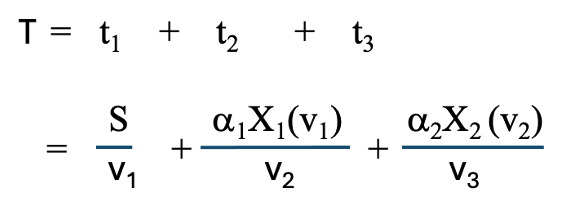
(3-2)
と示すことができます。
X1(v1), X2(v2)は事前に実験で調べておく関数です。またY3(F)も実験的に前もって調べておく関数です。この連載(3)では、連載(2)と同様に簡単な関数形で近似して、Tを最小にする、最適の研磨速度の時のv1,v2,v3,t1,t2,t3などの研磨の条件を考察します。
3-2-1. (A)式を用いた3段研磨最適条件
(A)式は連載(1)でPn = Xn (vn) = anvn と設定しています。 また、Y3(F) = v3 = F/a3 になります。これにより、Xn (vn)とY3(F)の関数の形が設定されます。(A)式は現象論的な式で、この式自体に物理的な意味はありません。
このXn (vn)とY3(F)を(3-2)式に代入して最適解を求めます。(3-2)式の第2項と第3項との部分での最適解は、2段研磨の際の最適解がそのまま使えます。2段研磨最適解は(1-6)式に示しています。ただし、(1-6)式のα1、a1、a2、Sは、α2、a2、a3、α1 a1 v1 に書き変えます。そうすると3段研磨の局所最適研磨時間、local minimum time、TLは、(3-3)式になります。(3-3)式の第1項は3段研磨の1段目の研磨時間、第2項は2段目と3段目研磨最適時間を示しています。
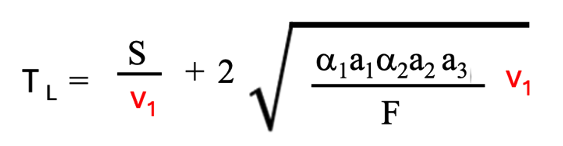
(3-3)
(3-3)式はv1の関数になっています。(3-3)式は(2-2)式と似たような式です。v1の増加に伴い第1項は減少し、第2項は増加します。v1を変数とするとTLのグラフは図2-2に示すような曲線になり、TLを最小値にするv1が存在します。(3-3)式のTが最小になる条件は、
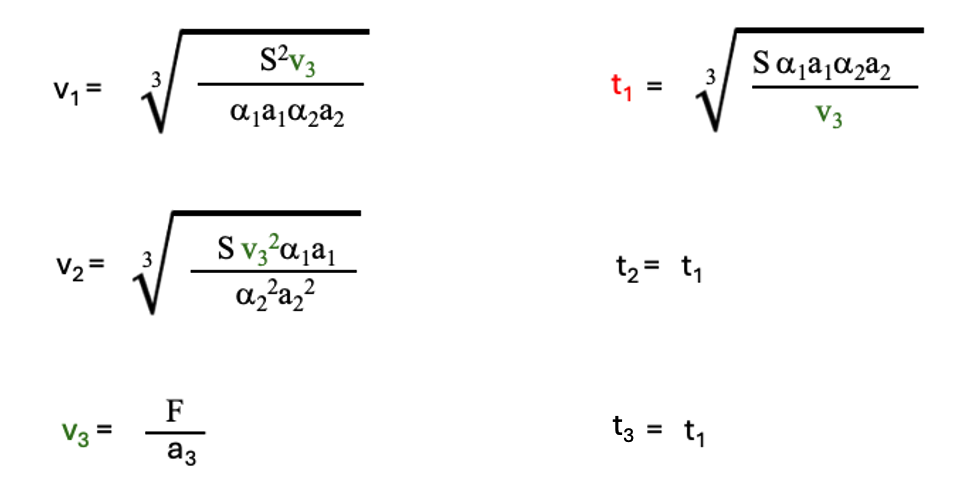
(3-4)
という最適研磨の条件が得られます。(3-4)式に示されているようにt1 = t2 = t3という結果が出てきます。そして、各研磨段の研磨速度も一意的に指定されています。この指定された研磨速度で、最適研磨が達成されます。各研磨プロセス後のウエハの洗浄時間WTを考慮すると3段研磨最適状態での研磨時間は

(3-5)
と表現されます。この結果は2段研磨の時の最適条件 (1-6)式からも容易に推察される結果です。
連載(2)の2段研磨の考察で、1段目の研磨では高速で研磨し、1段目の研磨の終了時に低速で研磨し、加工変質層を薄くして、2段目の研磨につなげるテクニックについて言及しました。これは実質3段研磨だと考えられます。この変速の2段研磨の場合、上記の(3-4),(3-5)式のa2をa1に書き換えると、このモデルの解は出てきます。この場合も最速条件では、1段目の高速で研磨する時間と、1段目の低速で研磨する時間は同じ時間に設定するという結論が出てきます。
1段目の研磨は粗い研磨で、2段研磨は1段目よりも粒径の小さな砥粒を使うことを想定しているので、普通はv1>>v2の条件で研磨を行います。(3-4)式は必ずしもv1>>v2になる条件は含まれていません。v1>>v2になる条件を求めてみると、
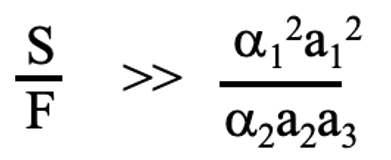
(3-6)
という前提条件が出てきます。この条件が成立するかどうかは、実際の数値を代入しないと明確にはならないのですが、通常はS>>Fなので、上の不等式が成立するようなSとFを選んで研磨の条件を設定します。上の不等式が成立しない場合は、3段研磨最適解(3-4)式の解の意味はなくなります。v2>v1の場合は、1段目研磨を省略した2段研磨が優位になって来ます。
次に、v2>>v3の条件を考察すると、下記の条件が出てきます。
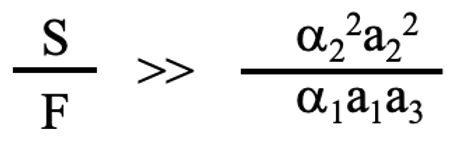
(3-7)
これも、実際の値をそれぞれのパラメターに代入しないとこの条件が成立しているかどうかは不明ですが、S>>Fの場合は(3-6),(3-7)の両方を満たすと推察されます。






