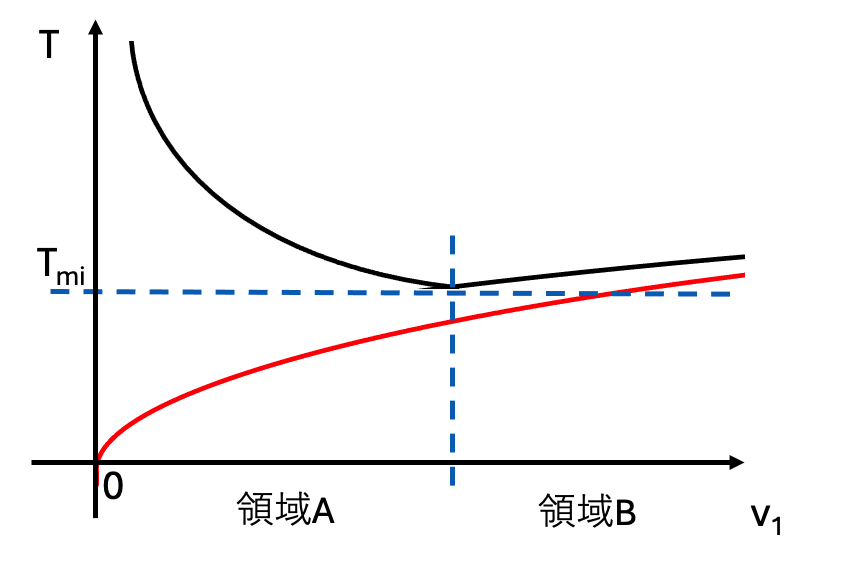
図2-2は、(2-2)式をグラフにプロットした図です。Tが最少になるところでは、t2= 2t1です。2段目の研磨では小さな粒径の砥粒を使う場合や、2段目はCMPを想定することが自然です。この場合、やはり通常v1 >> v2になります。この条件で研磨することを想定すると
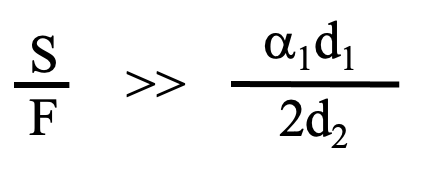
という条件が得られます。実際に数値を代入しないとこの条件が成立するかどうかはわからないのですが、通常はS>>Fなので成立しそうです。この条件を満さないときは、v2>>v1になります。その場合は2段目の研磨の条件で1段研磨を行うことが、速いことになります。S/Fの値に依存していて、S/Fが大きくなるほど2段研磨が優位になってきます。
2-4. 2段研磨での消耗量について
SiCの研磨では砥粒や研磨剤などの消耗が激しいことが知られています。そして、それらの消耗品は高価なのが研磨工程が高価になる理由の一つだと言われています。消耗品費が研磨条件に依存して、どうなるかを考察します。ここでは以下に示すモデルを想定して考察します。
n段目の研磨速度が速いほど、n段目研磨での消耗品の消耗量が大きくなると想定されます。またn段目研磨時間が長いと、やはり消耗品の消耗量が大きくなると考えられます。つまり研磨速度と研磨時間の両方に、消耗量が比例していると想定します。この想定を考えると、これは削り落としたウエハの厚みに比例して砥粒や研磨剤などが消費されると設定していることとします。これらの関係は、単に現象論的な関係だと考えておきます。実際の研磨では、研磨条件を一定にしていても、消耗量は一定ではなく次第に変化していくことが発生したりする事があるようですが、ここでは消耗量についての定性的に考察するので、そのような効果は考慮しません。実際の消耗状態は、消耗量を実験で測定し現象論的な関数を用いて表すことは可能です。企業では消耗量をPCでシミュレートし、消耗品費を予測していると思われます。
1段目の研磨の砥粒や研磨剤の消耗品の単位量の値段と消耗量とに対する比例定数をP1、2段目研磨の比例定数をP2とします。Pnの単位は[¥]/[L]とします。(A)式の場合を想定します。そうすると最速条件での消耗品費C(TM)は
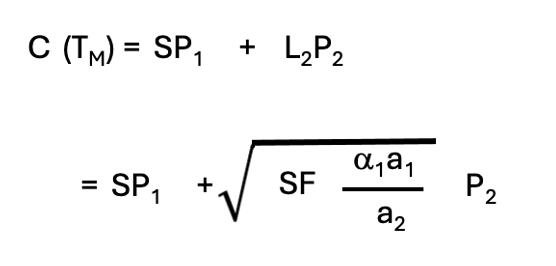
(2-5)
が出てきます。この連載の研磨モデルの想定では、C(TM)が最小値かどうかは不明なので、仮に研磨速度v1を変数として振ってみることにします。消耗品費は(2-6)式で示すことができます。当たり前ではありますが、(2-6)式の1項目はv1には依存せず常に同じ値です。2項目の研磨の消耗量はv1が遅いほど少なくなり、消耗品費C(v1)は小さな値になります。
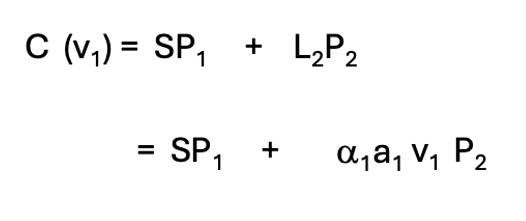
(2-6)
このモデルでは、研磨の高速化と、研磨に伴う消耗品の消耗量を抑えることは、互いに相反する目的だということがわかります。2段研磨で消耗品費をなるべく抑えるには、なるべく遅い研磨を行うべきということになります。(B)式の場合を想定しても同様な結論になります。そして余談的な話ですが、研磨の高速化と研磨に伴う消耗品の消耗品費を抑えることを両立させるには、より安価な砥粒や研磨剤の開発をしなければならないとの結論が出てきます。
消耗品費を抑制するとの観点からは、各工程での研磨速度を上げれば良いわけではない、との結論は得られます。研磨に伴う消耗品費を抑えるには、当たり前の結論ですが、余分な研磨はなるべく抑える、余分に高速な研磨はなるべく抑える、との結論は出てきます。その意味では、各工程の適正な組み合わせによって、無駄な研磨を抑えることは、ある程度は意味があるかもしれません。
研磨条件と研磨剤の消費に関する実験結果が、明確に示される実験結果が出てくると、消耗量と研磨条件の良い関係の使い方を見つけ出す可能性があるのかもしれません。そして、研磨条件と消耗量の関係の何らかの適切なモデルを設定すると、全消耗品費と研磨条件との関係をシミュレーションすることは可能だと思われます。
2-5. 2段研磨の研磨時間についてのまとめ
現象論的な式(A),(B)式を想定すると、2段の研磨のモデルでは研磨時間は(1-5)や(2-2)式で示すことができます。現象論的な近似式を使うと2段研磨での全研磨時間Tは、1段目の研磨速度v1の関数として表示できて、T(v1)をv1で微分すると、最速の研磨時間と最適な組み合わせが、どの辺りにあるのかが推察できて、研磨の律速因子を理解することができました。他のいつかの異なる現象論的な関数で考察した場合どうなるかを考察してみます。
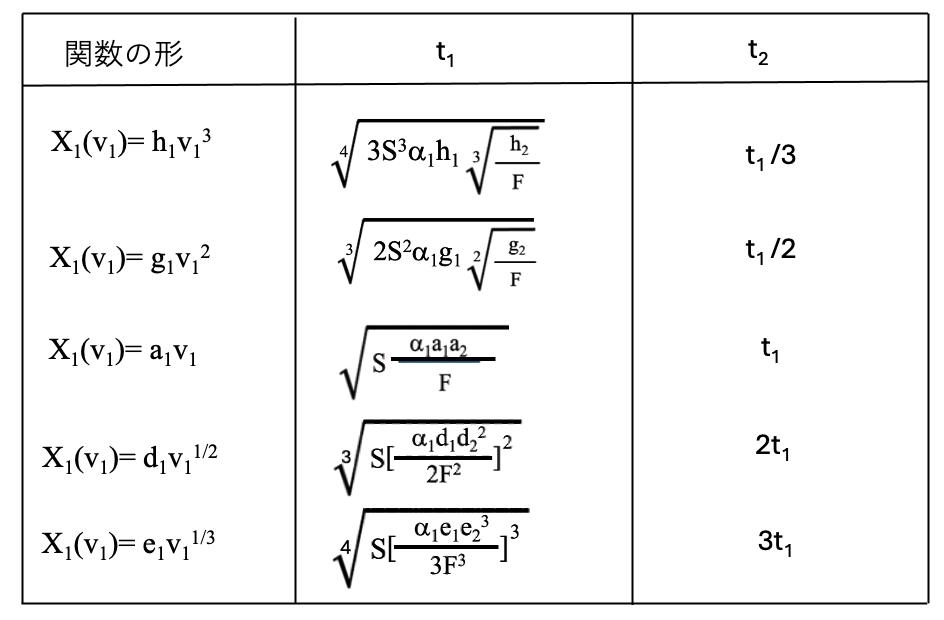
X1(v1)= a1v1, X1(v1)= d1v11/2, X1(v1)= e1v11/3,…… X1(v1)= e1v11/m,と関数の形を変えると、mをパラメターとした法則性のある結果が現れます。各関数形での適切な研磨条件は帰納法的に推測することができます。同様にX1(v1)= g1v12, X1(v1)= h1v13,……と仮定しても、各関数形での適切な組み合わせの研磨条件は帰納法的に推測することができます。それらの関数を使った結果、求めることができる研磨時間Tを描くと、図2-1から図2-2で示したグラフと似たグラフを描くことができて、他の関数形でも同様な考察をすることができます。これらの関数を変えた時の最適な組み合わせの条件も記述が可能ですが、単に数式の羅列のようなものなので、退屈な記述になると思います。それぞれの現象論的な関数を用いた最適研磨条件での、1段目の研磨時間t1と2段目の研磨時間t2をAppendixに示します。
適切な研磨条件を実際に見つけ出す場合は、このような解析的なことを考える必要はなく、エクセルなどのPCソフトを使って実際の実験データーを整理するとX1(v1)やY2(F)などの関数は決定することができます。(1-5)式などを使ってT(v1)の値を計算することは可能です。v1を変数として計算するとT(v1)の最小値を見つけ出すことができて、さらに各段の研磨速度、研磨時間もPCの力技で簡単に見つけ出すことは可能です。この解説文で解析的な解を使って、議論している理由は、各段階の研磨速度を変えると全研磨時間がどう変化するのか、それぞれの研磨の条件で何が律速因子になっているのか、最適条件では何が起こっているかなどを考察しているためです。
このようなことを書くと、加工研磨の研究者からは、実験でαnXn(vn)などを見つけることは大変な作業だ、そんなに簡単な作業では無いと言われそうです。それはそうなのですが、加工研磨の研究者は、通常、研磨条件を変えて表面を光学顕微鏡やAFMで表面の荒さを測定しています。AFMでRMSの値を調べ、RMSの値が収束して落ち着いった時の研磨条件を探し出します。このとき、少し余裕をもってさらに研磨を行って最適研磨条件を導いています。この作業自体は、αn-1Xn-1(vn-1)を推定している作業です。そして、研磨レシピを作成する際には、いくつかの条件を変えてαn-1Xn-1(vn-1)をいくつか調べることを行います。通常の研磨レシピを探索するやり方とそれほど離れたことを行う訳ではありません。そして、これらのパラメターをさらに精度良く求めるためには、さらなる計測方法の工夫が必要だとは推察します。特に、αnの値をさらに詳しく実験的に求めるやり方は、この連載の後の回で考察します。
2段研磨で行う方が優位なのか1段研磨が優位なのかを判断するクライテリオンを考察しました。F/Sが重要なクライテリオンになることを示しました。通常、多段研磨を行なって、最終的にCMPでウエハの研磨を仕上げています。近年はこの最終段のCMPはかつて、CMP 1段研磨を行なっていましたが、近年は、CMP 2段研磨を行うようになってきているようです。CMPを2段研磨で行う方が優位なのか1段研磨が優位なのかは、CMP研磨で削る目標の厚みと、仕上げの際に残存する加工変質層の厚みの比、F/Sが重要なクライテリオンになると考えられます。
上記の(A),(B)式のように、加工変質層の厚みが、研磨速度の関数として示されていることから、1段目研磨では高速で行い、1段目研磨終了時に研磨速度を落としてしばらく研磨すると1段目研磨での加工変質層の厚みを薄くすることができて、2段目につなげるというテクニックも考えられるかもしれません。1段目の研磨で研磨速度を変化させるやり方です。そうすると、より高速で研磨できるかもしれません。これは結局のところ3段研磨です。
次回の連載(3)では3段研磨の最適な組み合わせの研磨条件について考察します。この連載で示している内容は、こういうモデルで考えると、こういう結論が出ます、ということを書いていることを了承して下さい。
(つづく)
Appendix
2段研磨で、研磨速度と加工変質層の厚みの関係を関数で表示した場合、関数の形と、最適研磨条件での1段目の研磨の時間t1と2段目の研磨の時間t2との関係の表