アイシーソルーションズ, LLP

2-1. はじめに

SiCウエハの加工研磨工程を統合化した場合の、最適の組み合わせについて考察しています。前回の説明では、2段研磨での、最適条件を導きました。そして、2段研磨についての考察の途中で話が終了しました。

前回は、研磨速度と加工変質層の厚みの関係を、現象論的ないくつかの近似式を想定して考察ました。前回で示した現象論的な式、(1-2),(1-3a)の2つを取り出して、これらを雛形の関数として使い、連載(2)では話を進めます。これらの2つの式を簡単に示すために、(A),(B)式と名づけることにします。

P_n = X_n(v_n) =  a_n v_n 　　                　　 (A)

P_n = X_n(v_n) =  d_n v_n^1/2     　　　　　　(B)

P_nはn番目の加工研磨で導入された加工変質層の厚みです。加工変質層の厚みは実験によって求められるのですが、加工変質層の厚みは、ウエハ表面の各位置で変動していると考えられ、実験によって求められる厚みはそれらの平均の加工変質層の厚みと考えられます。X_n(v_n)は近似的で現象論的な加工変質層の厚みを表していて、研磨速度v_nの関数と設定しています。a_n, d_nは比例定数です。この(A)式(B)式を用いた2段研磨の解について、考察を進めます。

現実の研磨では、研磨の状態が一定に保存されていないことが発生することがあるようです。研磨装置のターンテーブルの回転速度を一定にし、研磨の負荷応力を一定にして、研磨を継続しても、複雑な理由により、次第に研磨速度が落ちてくる現象などが発生することがあるようです。この一連の解説文では、まずは簡単な研磨モデルを想定していて、解析的なモデルを用いて定性的な議論を行います。一方、PCを使ってシミュレーションを行う場合は、研磨条件が研磨時間に依存して次第に変化するモデルを使うことは、容易に可能かと思います。研磨速度の減少は簡単な現象論的な近似式で十分だと思われます。あるいは、研磨速度を一定に保つ自動制御装置付きの研磨装置を想定して考察していると、考えてよいかもしれません。

そして、この解説で示す研磨モデルは、研磨表面直下に存在する加工変質層の厚みが、全体の研磨時間に大きな影響を及ぼすというモデルで考察します。

2-2. (A)式を用いた2段研磨の適正条件

連載(1)では(A)式を使って2段研磨の研磨時間Tを考察しました。2段研磨の研磨時間は、

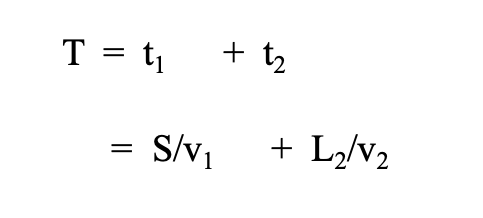
です。Sは1番目の研磨で削り落とす厚み、L₂は2番目の研磨で削り落とす厚みです。t₁,v₁,t₂,v₂はそれぞれ1段目と2段目の研磨時間と研磨速度です。これを書き変えると

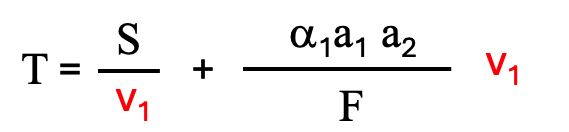
(1-5)

上記の式は連載(1)の(1-5)式です。Fは最終的に2段目の研磨で残留する、薄い加工変質層の厚みです。このFは最終目標の加工変質層の厚みです。α₁はアクシデンタルに導入される傷に対応するための安全係数です。v₁の増加に伴って(1-5)式の第1項は減少し、第2項は増加します。(1-5)式で示される1段目の研磨での研磨速度v₁と2段の全研磨時間Tの関係を下記の図2-1に示します。

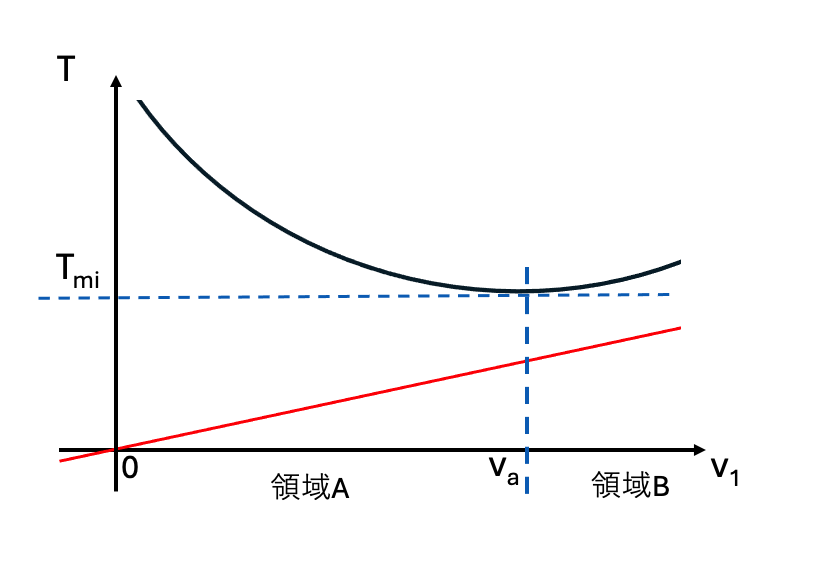
(1-5)式で示される1段目研磨の研磨速度v₁と全研磨時間Tの関係は双曲線で示され、全研磨時間の最小値T_miとこの時の1段目研磨の研磨速度v_aが求められます。この曲線は赤い直線で示す漸近線に接近していきます。この漸近線は(α₁a₁a₂)/Fの傾きがあります。0からv_aの間の領域Aの部分では、t₁>t₂の領域で、t₁がTを律速しています。この領域では１段目の研磨時間t₁=S/v₁の双曲線グラフの形が現れています。v₁が大きくなるとTは減少します。1段目の研磨で導入される加工変質層の厚みP_１はv₁に比例して大きくなるモデルで考察しているので、v₁が大きくなると2段目の研磨作業で削り落とさなければならない厚みが直線状に増えていきます。Tの最小値では、t₁=t₂になっています。図2-1の領域Bではt₂>t₁になっています。

連載(1)で求めたように、適切な条件での全研磨時間は2回の洗浄時間WTを加えて

(2-1)

が得られます。2段研磨を行う時に単純に想定されることはv₁>>v₂での研磨です。2段目の研磨速度が1段目の研磨速度よりも速い場合は、最初から2段目の研磨条件で研磨を行う1段研磨で充分です。このv₁>>v₂の研磨速度の関係が成立するのは以下のような条件です。

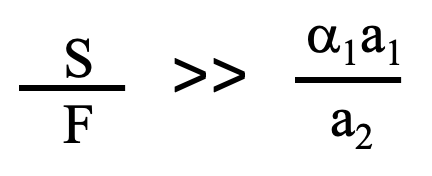
この条件は各パラメターに実際の数値を代入しないと成立するかどうかは不明ですが、通常はS>>Fです。S/Fの値が小さくなってくると、2段目の研磨速度が1段目よりも速い状態になって来るので、最初から2段目の研磨のやり方で1段研磨を行う方が次第に優位になって来ます。

X_n(v_n) =  a_n v_n (A)式を想定した、研磨速度と加工変質層の厚みの関係を想定して2段研磨の研磨時間を考察すると、v₁の関数として図2-1のようなグラフを描くことができました。次に、 (B)式を使った例で考察します。

2-3. (B)式を用いた2段研磨の最適条件

連載(1)で示した(B)式を使うことを考えます。(B)式は下記のような近似式です。

P_n = X_n (v_n) = d_n v_n ^1/2             

(B)

ここでv₂ =Y₂(F) = (F/d₂)² で示されます。v₂はFによって固定されています。

そうすると2段研磨の時間は以下で示されます。

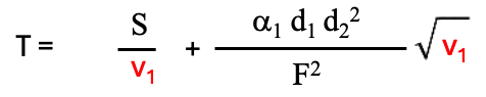
(2-2)

Sは1段目の研磨で削り落とす目標の厚み、Fは2段目の仕上げ研磨によって形成される最終加工変質層の厚み、つまり目標とする仕上げの状態です。v₁の増加に伴って(2-2)式の第1項は減少し、第2項は増加します。2-2. 節で述べたやり方と同じやり方で以下のような結果が得られます。

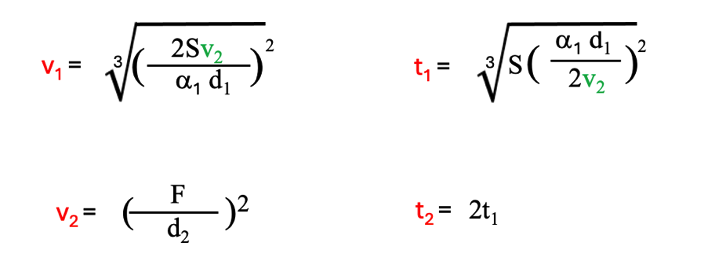
(2-3)

(B)式の関係を想定する条件では、2段目の研磨時間は1段目の2倍の時間を必要とすることがわかります。この結果は(A)式の結果とは異なる結果です。そして、1段目と2段目の研磨速度は一意的に指定されています。

洗浄時間WTを含めた2段研磨での研磨時間は

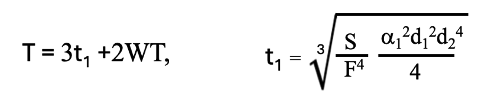
(2-4)

と示されて、整った解が求められます。

ページ : 1 2