9.単斜晶構造
さて、本記事では立方晶、六方晶、三方晶の結晶を順に取り上げてきたが、最後に紹介するのがβ-Ga2O3が属する単斜晶の結晶である。結晶を形作る平行六面体の内、最も対称性が低いものが三斜晶であるが、単斜晶はそこに格子定数の関係としてα = β = 90˚(或いはα = γ = 90˚)を課したものである。対称性としては他の2個の基本並進ベクトルに共に直交する基本並進ベクトルに平行な2回回転軸が現れる。この構造を積層構造と親和性が良いように2次元ネットから構築しようとすると、一般的に図4-7の様な2通りの表現が可能である。一つは(1)斜方ネットをもとにしてそれをネット面に垂直に積み上げる方法、もう一つは(2)長方形ネットをもとにそれをネットの基本並進ベクトルの一つ沿ってシフトさせた上で積み上げる方法である。いずれもBravais格子としては同じ斜方格子が出来上がるが、本図において (1)では斜方ネット面に垂直な積み上げ方向をb軸、(2)では長方形ではないa-c面(b面)の一辺となる積み上げ方向をa軸としており、共にβ ≠ 90˚となることに注意願いたい。
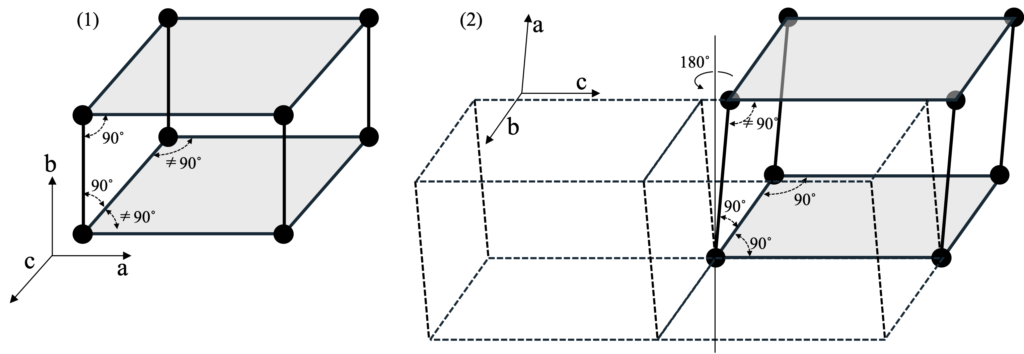
エピタキシャル層状成長を層の積み重ねと考えた時、最表面の対称要素として上記いずれの場合も2回回転軸がある。その構造情報だけを上層が引き継いで単斜格子が出来上がると、(2)の場合は図4-7(2)で示すような2種類のドメイン形成が考えられる。格子点に配置される基本要素内の結合の方向性等による制約がない限りこの両ドメインは等確率で発生すると考えられ、その間では並進対称性が保たれなくなっている。このような状況から、単斜晶系の結晶のエピタキシャル層状成長で欠陥の少ないものを得ようとすると、(1)のように成長面が斜方ネットであって結晶のb軸方向がその成長面(ネット面)に垂直であるように成長面を選ぶのが望ましいと思われる。
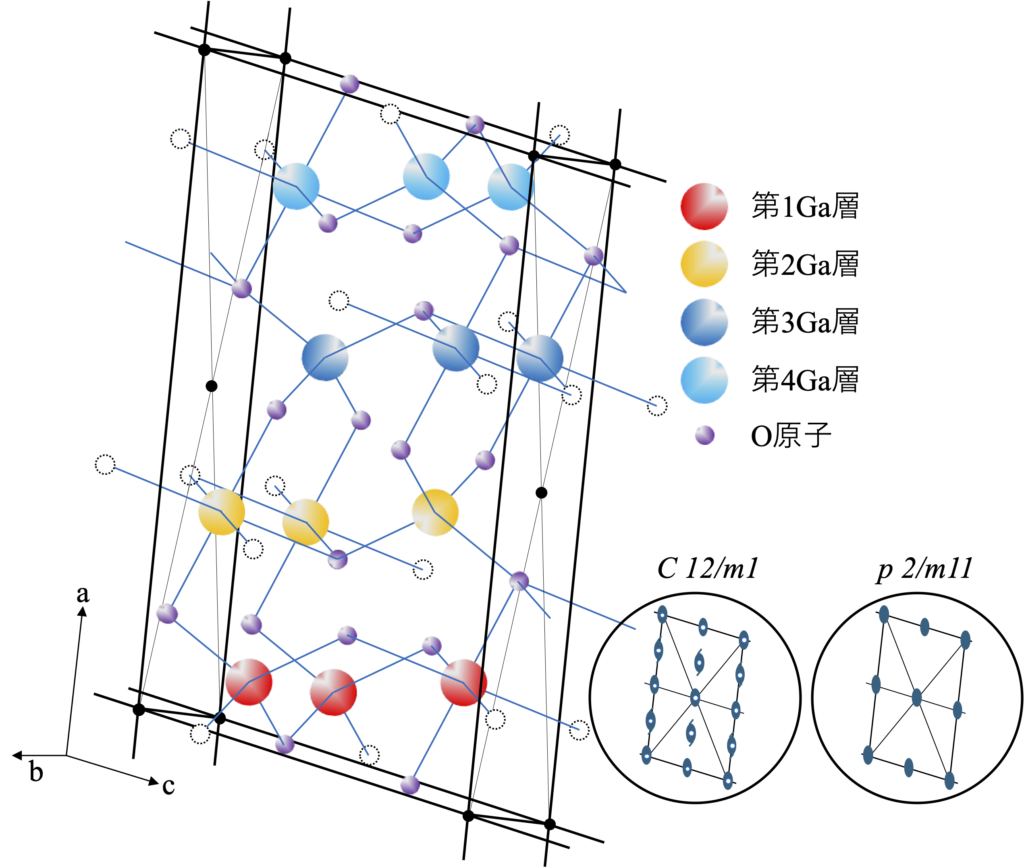
次にβ-Ga2O3を例にしてもう少し詳しい検討をしてみよう。β-Ga2O3の結晶構造9)は他の構造と比べて複雑であり分かり易く図示するのが些か難しいが、改めて模式的に書き表したのが図4-8である。構造が理解しやすいようにGaを大きめ、Oを小さめの丸で描いているが、特徴的なのは、今までの半導体材料でも見られたような四面体構造と八面体構造がGa原子を重心にしてユニットセル内に1:1で存在している(他の半導体では片方のみ)ことである。但しこれらは正多面体ではなく若干歪んでおり、相互に頂点或いは辺を共有するのみで面は共有していない。ユニットセルは図4-8のようにC底心格子(a-b面の中心に格子点)として定義出来るが、その場合格子点には原子は存在しない。格子定数的にはβ = 103.7˚、b:c:a ≅ 1:2:4で軸長間の差が比較的大きい。これらの軸長は、その軸に沿って積層しているユニットセル内の原子層の数に対応しているとも考えられる。また格子点に対応した基本要素の単位はGa4O6であり、C底心格子の構造に対応してユニットセル中には2単位存在する。
ここで結晶面上への積層構造を考えてみることにしよう。まずa-c面上の場合であるが、図4-7(1)に相当する。成長時の単位となる層はほぼ図4-8のユニットセルそのものであり、それがb軸方向にそのまま積層できる状況である。頂点を共有する四面体構造、及び辺を共有する八面体構造の結合手がb軸方向にジグザグに連なっており、a-c面内でシフトする事無しに積層が可能である。この状況はFCCの<111>方向に類似している。しかし、層としてのユニットセルが極めて大きく、多くの原子を含んでいることもあって層内の複雑な構造(層内の対称要素は2回軸のみ)を正確に再現するのに些か骨が折れるかもしれない。
では、b-c面上成長はどうであろうか。こちらは図4-7(2)に相当するケースであり、a軸が成長面であるb-c面に垂直とはならない。そのため、図2-7(2)で述べたように異なるドメインを生成し易いであろう。積層構造的にはユニットセルは4層から成立することになるが、2層目、4層目の層構造は1層目、3層目をb軸の周りに180˚回転させたものになる。結合手の方向から積層する際に層内でシフトすることが必要であるが、酸素原子の結合手の方位が安定でなく多面体構造がひずんでいることにも起因してc軸方向のシフト量が層間で一定となっていない。HCPベースの結晶のケースで見られたエラーを引き起こす層構造の変換と考え併せると、c面上への積層では欠陥発生の確率がかなり高くなるのではないかと予想される。
このように考えると、本記事で取り扱った他の半導体結晶と比べると、β-Ga2O3の欠陥の少ない高品質結晶成長にはその構造を安定化させる何か特別のドライビングフォースが必要であり、それを見つけて制御することが何にもまして重要であろう。(201)面の最表面の構造がウルツ鉱型の(0001) に擬似的に似ていることが知られており、何かうまく活用する道があるかもしれない。







コメントを残す