アイシーソルーションズ, LLP

８．コランダム構造

　コランダム構造は、アルミナ（Al₂O₃）やα-Ga₂O₃などX₂Y₃の組成を持つ物質の結晶にしばしば見られる構造である。ルビーやサファイアの結晶がこの構造をもつことはよく知られている。前節において、六方格子における積層構造をもとに菱面格子の三方晶系の結晶が出来上がることを15R-SiCを例に解説したところであるが、同じく三方晶系に属するコランダム構造はどのような構造であろうか。

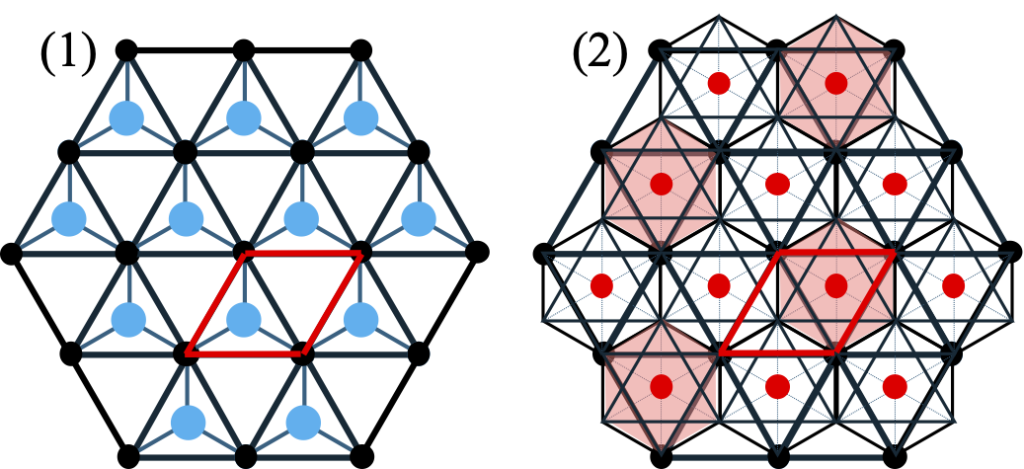
　本連載の2回目の記事で概説しているが、ここで改めてコランダム構造の詳細を見てみよう。今まで述べてきたHCPベースの結晶構造はHCPと正四面体構造から形作られるが、コランダム構造の基本はHCPと正八面体である。2次元の六方ネットとその格子点の空孔に存在する正四面体、正八面体の関係を図4-4に示す。この図では正四面体サイト、及び正八面体サイトの重心位置を水色の丸と赤い丸で表しており、層内位置としては黒丸が格子点のAサイト、水色丸がBサイト、赤丸がCサイトに対応している。2層目の（２次元ネットとしての）格子点はBサイトにシフトし、以後AサイトとBサイトを交互に繰り返すウルツ鉱型の配置を取る。但し、紙面に垂直なc軸方向の位置は、層間距離に対して、水色丸は1/4、赤丸は1/2であることにご注意いただきたい。正八面体構造では、層内の位置は正四面体構造のケースで言うCサイトであるが、高さが違っている。{1120}面での断面を図4-5に示すが、正四面体構造から出来上がるウルツ鉱型と正八面体構造を取るコランダム型の原子配置の違いが、連載第２回の図2-4も併せてご覧頂くことでよくわかるであろう。このような状況を考慮し、同じHCPベースの構造ではあるが、コランダム型では正八面体構造の重心に位置する空孔からなる層（図4-5(2)の緑丸の層）も1層として扱うことにする。そうすると、層内座標が(0, 0)、(2/3, 1/3)であるHCPの最密充填サイトが六方ネットにおけるA及びBサイト、正八面体サイトがCサイトに相当することになり、原子YをA, Bサイト、原子XをCサイトすべてに配置した結晶ではACB’C’が1周期の積層構造であることになる。この構造がコランダム構造の親戚として知られているヒ化ニッケル構造である。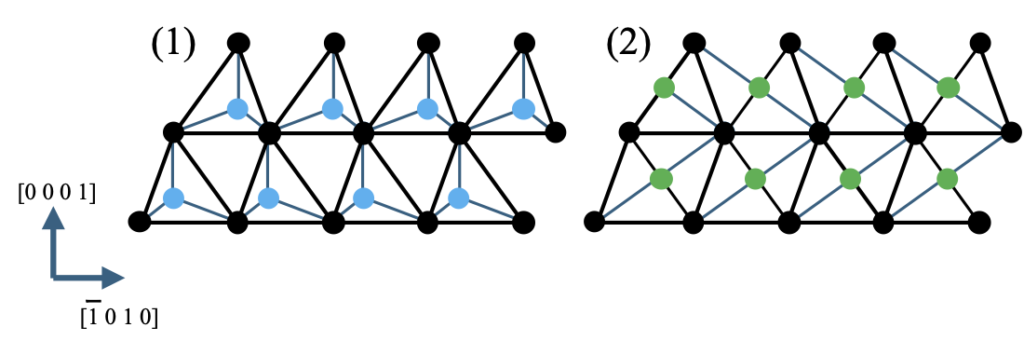ウルツ鉱ではCサイトには原子が存在しなかったが、この構造では最密充填サイトを頂点とした正四面体構造の重心に原子が存在しない代わりに、正八面体構造の重心に原子が配置されている状態である。

　さて、このままであれば全体の結晶構造は4層周期ということになるのであるが、コランダム構造では物質の組成が1：1ではないことから話しが少しややこしくなる。上記ACB’C’であれば4H-SiCと同様その結晶系は4Hで六方晶ということになる。しかし、Cサイトを占めるX原子（Ga₂O₃で言えばGa）の組成比がY原子（Ga₂O₃で言えばO）の2/3であることから、Cサイトでは1/3の割合で空孔が発生することになる。実際、CサイトのX原子からなる層を取り出してみると、図4-6の様なハニカム構造を取ることがわかっている。この結果、Cサイトが三種類出来ることになり、これをC₁, C₂, C₃サイトとすると、全体の積層構造は原子種を無視すればAC₁B’C₂’AC₃B’C₁’AC₂B’C₃’ と言うように、1周期が12層で構成されねばならないことになる。先に菱面格子がどのようにして形成されるかを示した。擬似的な基本周期ACB’C’でCサイトの軌跡をたどってみるとよく理解できるが、4層ごとにC₁→C₂→C₃→C₁という様に移り変わり、まさに菱面格子ができあがった15Rのケースに極めて類似している。Ramsdell表記で言えば、4層×3で12Rの構造ということができる。

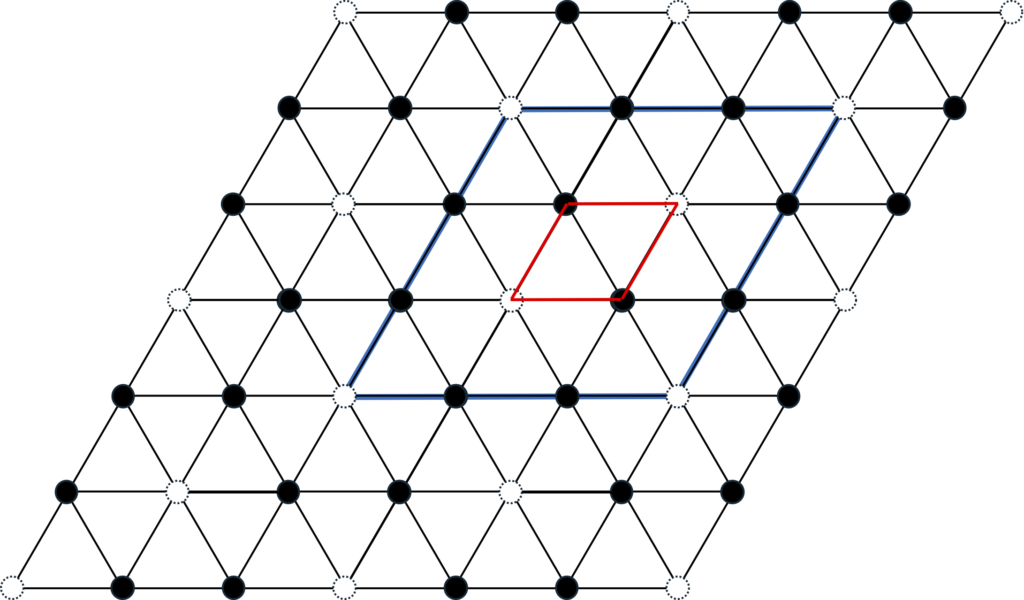
　以上、コランダム構造がどのようにして菱面格子になるかを解説したが、結果として12層周期という極めて長いc軸長をもつことになる。15R程ではないが、これだけ長い周期の結晶を人為的に作成するには、先にも述べたような周期性を維持させる何か特別のドライビングフォースが必要となろう。更に、X原子の層における1/3欠損であるが、図4-6のような規則正しいハニカム構造を一つの層の中で正確に作り上げるのにも結晶工学的にはかなり労力がいるのではないかと思われる。

ページ : 1 2 3 4