前回の第2回記事では、結晶の対称性の観点から各種半導体結晶の特徴と関連性を概説し、FCCベースの立方晶結晶を対象に対称性の違いによる欠陥発生を考察した。それに引き続き今回はHCPベースの六方晶及び三方晶結晶を対象にして同様の議論を行いたい。まず、六方格子と結晶系の対応を述べた上で、菱面格子、立方格子との相互関係を概観する。その後、HCPベースの結晶構造の詳細を対称性の観点から比較し、欠陥発生の違いを考察する。
5.六方晶系と三方晶系
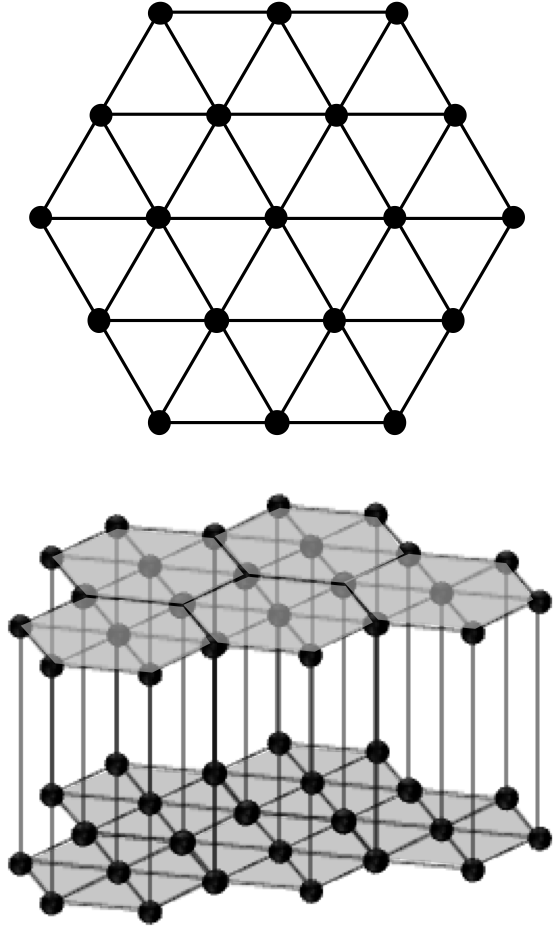
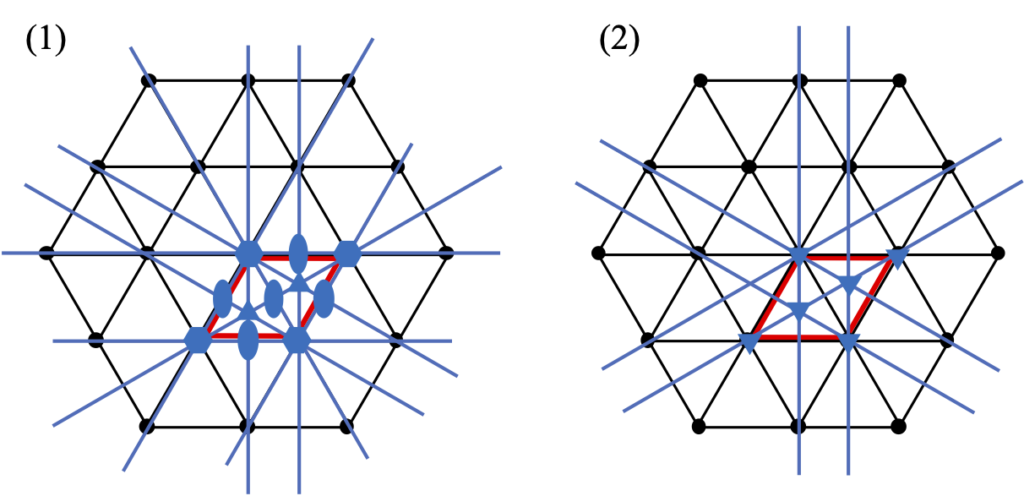
結晶系の話しをする際に、しばしば混乱が見られるのが六方晶系と三方晶系の区別である。六方晶系と三方晶系の本質的な違いは結晶の対称性、即ち6回対称軸(回転、回反、らせん)があるのが六方晶系、3回対称軸があるのが三方晶系となる。実はこの両者の格子構造は同一であり、図3-1に示すような2次元の六方ネットが紙面に垂直に重なって六方格子(格子定数で表現すればa = b ≠ c, α = β = 90˚ γ = 120˚)が出来上がっている。3回及び6回の回転軸の効果は60˚回転を2回繰り返せば120˚になることから一見前者は後者に含まれるように見えるが(実際、並進対称性のために格子にすると同一)、格子点に配置する基本構造の点群としての対称性が3回回転軸であれば、全体として3回回転軸となる。図3-1の六方ネットの格子点に6回回転軸、及び3回回転軸が存在した場合に、六方ネットに出現する対称要素を書きだしたものが図3-2であるが、この図に対称性の違いが如実に現れている。赤枠で示された基本ユニットセルの(2/3, 1/3, 0)と(1/3, 2/3, 0)の位置に3回回転軸が現れるのは同じであるが、(1) では基本ユニットセルの中心と辺上に2回回転軸が現れる。更に鏡映面としても(1)では{1 1 0}面が追加される。
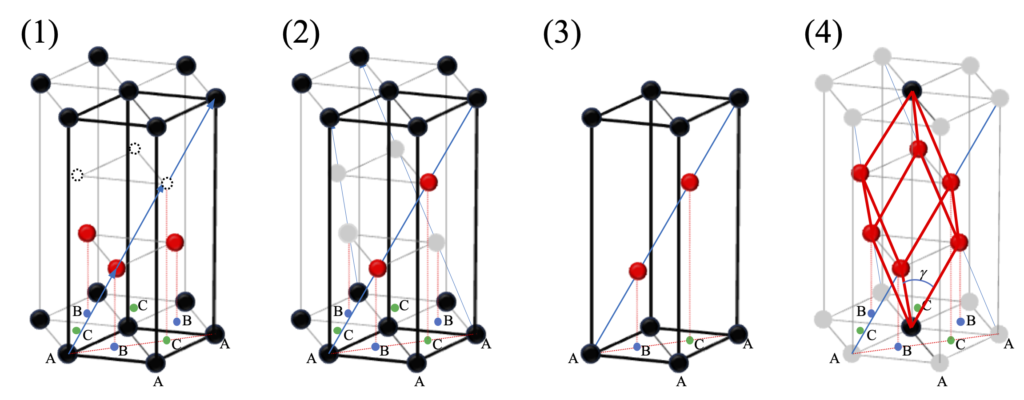
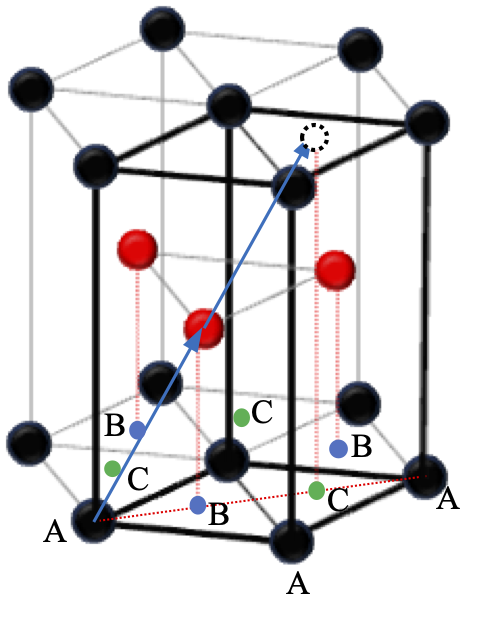
さて、ここで改めて菱面格子と六方格子並びにHCP構造の関係を見返してみよう。図3-3によく知られたHCP構造での最密充填原子配列を示す。太黒枠が単純六方格子の基本ユニットセルである。黒丸と赤丸が原子を示している。この図では単純六方格子の格子点は黒丸原子の位置に重なるように定義している。赤丸の位置も一見格子点であるように見えるが実はそうではない。格子点の定義から格子点間を結んだベクトル(並進ベクトル)の整数倍も並進ベクトルになるはずであるが、赤丸の位置を格子点としても左下の黒丸の格子点との間を結んだ赤矢印で示すように、それを2倍した場所には格子点が存在しないからである。
では、図3-3の赤丸と白丸の位置を格子点とするためには格子全体の構造はどのようになるべきであろうか。改めて描き直したものが図3-4 (1)である。言ってみれば図3-3の青矢印、その2倍、及びその3倍の位置を格子点とし、そこに原子も配置すれば並進対称性との両立が可能となる。その格子が図3-4 (2),(3)であり、単純六方格子3個からなる複合格子、即ち菱面六方格子と呼ばれるものである。この際、層と層の間隔(c軸長の1/3)には格子構造的に特別な制約はなく、赤丸のa-b面内での位置だけが重要である。そして通常描かれる六角柱の中に、3個の菱面六方格子を120˚ずつ回転させて配置すると、図3-4(4)のような基本並進ベクトルを再構成することができる。これが単純菱面格子である。即ち、単純六方格子を(1/3, 1/3, 1/3), (2/3, 2/3, 2/3)だけシフト(原点を図-3-4(3)の左下の格子点として)させた副格子と合体させた複合格子の基本並進ベクトルから再構成される単純格子が三方晶系として扱われる単純菱面格子となる。菱面格子は六方格子としての表示も可能である一方、六方格子で表現される構造全てが菱面格子で表示可能であるわけではない。
ところで、図3-4(2)の構造はFCCの<111>方向をc軸として捉えて、それに垂直な面を積層させたものと極めて類似していることにお気づきであろうか。実は立方晶系に属する単純立方格子、FCC更にはBCCも菱面格子の一種、と言うよりそれぞれの基本並進ベクトルが、菱面格子(格子定数的には、a = b = c, α = β = γ)の中で特別に対称性が高い場合(γ = 90˚, 60˚, 109.47˚)なのである。この意味で、原子層としての積層構造を比較議論する際には立方晶結晶も六方格子として表示させることが可能で、その方が理解もし易い。特にFCCの場合には、菱面格子の基本並進ベクトル長がもとの六方ネットの基本並進ベクトル長と等しくなり、図3-4(3)の底面の3個の黒丸とその直上の赤丸が正四面体構造を取る。以後、最密充填層の積層として結晶構造を考察する際には、立方晶の<111>方向を六方晶<0001>方向と対応させ、六方格子のc軸に垂直な面内において上下層との関係で原子の最密充填配置が可能なサイトを図3-4に示すようにAサイト、Bサイト、Cサイトとする。