Appendix 2(1, 3)
- 結晶内の面、方位を表すMiller指数, Miller-Bravais指数
結晶や格子の議論をする際、結晶内の面や方向を表すのに使われる指数。結晶格子のユニットセルの並進ベクトルをa, b, cとした時、格子点を結ぶ方位ベクトル r がr = ha + kb + lc(h, k, lは整数)で表されるなら r の方位の指数を[h k l ]と表す(通称、定数倍して簡単な整数比になる値を用いる)。対称性から等価な方位は<h k l >で表す(例えば、単純立方格子で<100>は、[100], [100], [010], [010], [001], [001]の総称)。各指数が負の数の場合は [h k l ] の様に上付きバーを付けて正の数で表すのが通常であるが、印刷等の都合で [-h k l ] と記載されることもある。
結晶格子のユニットセルの並進ベクトルをa, b, cとしてそれぞれの単位長で座標軸を設定した時、ある面(平行な面は等価と考える)の座標軸切片が1/h, 1/k, 1/lである場合、その面の指数を(h k l )で表す(方位指数と同様、通常は定数倍して簡単な整数比になる値を用いる他、負の数の扱いも同様)。対称性から等価な面は{h k l }で表す。これらの方位と面の表し方をMiller指数と呼ぶ。
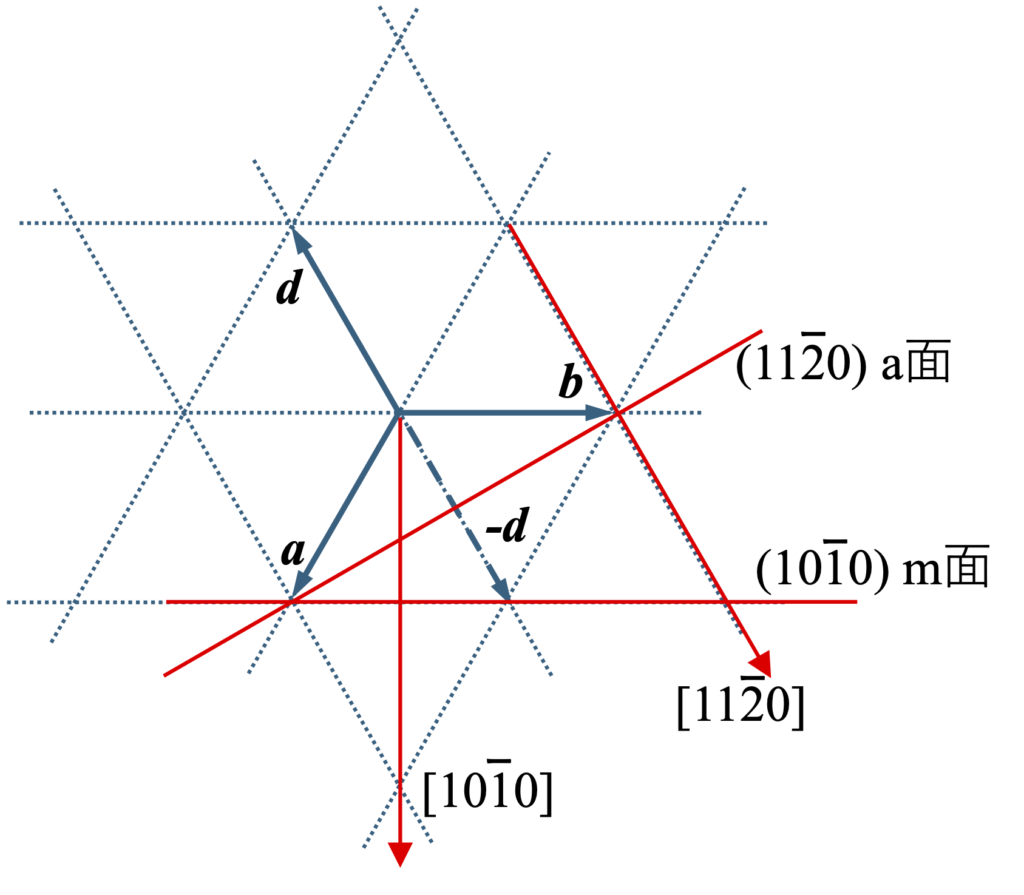
六方格子の場合は、a-b面内の基本並進ベクトル間の角度gが120˚であるため、面内の第3のベクトルd = -(a + b)を用いてb, d, c或いはd, a, cを基本並進ベクトルと定義することも可能であり(下図参照)、これらの設定は全て等価である。この状況から対称性を分かり易くするため、(hk l)面は指数を4個として(hk i l)のように表す。h + k + i = 0の関係がある。方位では、[u v w]は[(2u–v)/3 (2v–u)/3 (-u–v)/3 w]のように変換される。これら4指数の表記をMiller-Bravais指数と称する。
- 結晶対称性の対象となる対称操作(対称要素)とは
ある格子点を不変とする回転、回映、鏡映、回反、反転の点対称操作、基本並進ベクトルの整数倍である並進操作、及び点対称操作と基本並進ベクトルの分数倍を組み合わせたらせん、映進がある。それぞれの対称操作のイメージは下記を参照。回転関連の対称操作を特徴付けるnに関して、結晶の並進対称性と両立するnの値は1, 2, 3, 4, 6のみである。

対称要素の表記法として、Schönflies表記とHermann-Mauguin表記(国際表記)がある。上記のうち、Cn, Sn, σ, i はSchönflies表記、n, n, m, nq, c, n(nグライド面としての)はHermann-Mauguin表記である。各対称要素の慣用的に用いられているグラフィカルな記号を以下に示す。

数学的には、点対称操作は結晶点群、並進操作は並進群、対称操作全体は空間群と呼ばれる群構造をもつ。結晶点群は32種、(3次元)空間群は230種、(2次元)平面群は17種、層群は80種存在することが知られている。
- 点群、空間群の表記法(Hermann-Mauguin表記)フルシンボルとそれを当該の群を規定するのに必要な最小限の対象要素だけに簡略化したショートシンボルがある。
Lαβγ:点群ではLは記載なし
- L:ユニットセルを形作るBravais格子の種類(P, I, A, B, C, F, R)ー 空間群では大文字、平面群/層群では小文字で表現
- α:主軸周りの対象要素(通常[001]軸を主軸とする)
- β:結晶系によって決まる主軸とは異なる軸周りの対象要素
- γ:結晶系によって決まる更に別な軸周りの対象要素
α, β, γ で、その軸に垂直な鏡映面、映進面があれば /m や /c 等を軸周りの対象要素に追記。主軸以外に対象要素がなければβ, γは省略される。





