4.FCCベースの半導体結晶(SiとGaAsの違い)
それでは、上記で述べてきた各結晶構造の特徴を踏まえ、個別の半導体の結晶構造をエピタキシャル成長を念頭に置いた層構造の点から考察してみたい。まず代表的な半導体結晶であるSiとGaAsついてその(001)面について見てみよう。結晶構造的には、Siはダイヤモンド構造、GaAsは閃亜鉛鉱型構造であり、前者は結晶構造の中でも最も対称性の高い空間群に属する。共にFCCがベースで、その格子点に基本構造として原子1(座標(0,0,0))+ 原子2(座標(1/4,1/4,1/4))を配置すると結晶が出来上がる。原子1と原子2が同じ場合がダイヤモンド構造、異なる場合が閃亜鉛鉱型構造である。原子1も原子2も”結合手”を4方向に出しており、結晶中で原子1の正四面体構造の重心に原子2、或いは原子2の正四面体構造の重心に原子1が存在する構造となっている。
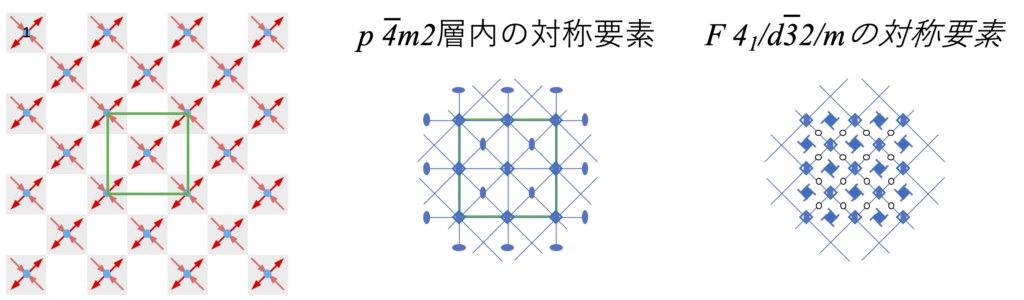
4m2)、及びその対称要素。緑の矩形は3次元構造に対応させた面心正方形ネット(基本ユニットセルは単純正方形ネット)のユニットセル。参考にダイヤモンド構造(F 41/d32/m)のc軸に垂直な面から見た対称要素の一部も示す。左図の赤矢印は原子のsp3混成軌道からなる”結合手”を表し、その向きは紙面上方を表す。 ここでc軸に垂直な層の積層構造として考えると、そのユニットセルは4層構造で各層の構造は同一(図2-6を参照、層群的にはp 4m2と表現される。)であるが、第2層と第4層((原子2からなる)は第1層と第3層(原子1からなる)を層自体を鏡面として鏡映操作したものである。積層の際には共有結合の方向性から、上層は下層に対してa-b面内で順次(1/4, 1/4), (-1/4, 1/4), (-1/4, -1/4), (1/4, -1/4)だけ平行移動した場所に位置する。この様子を図2-7に示す
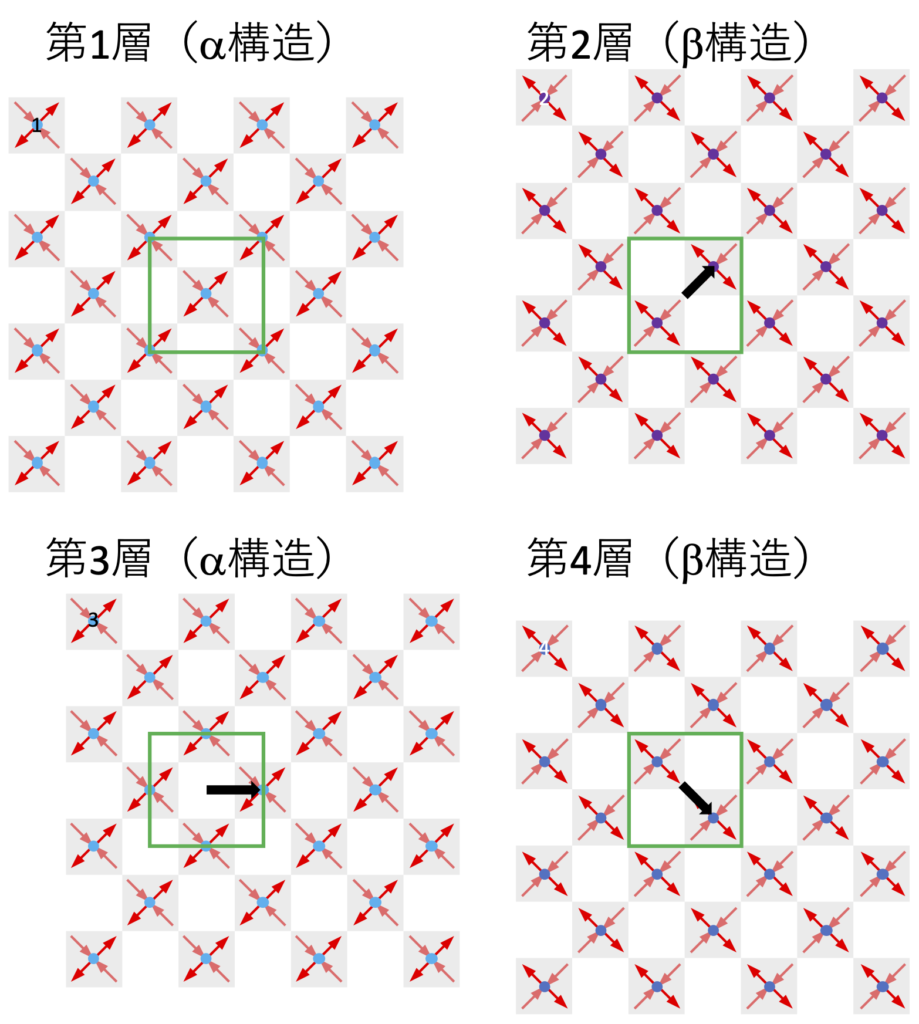
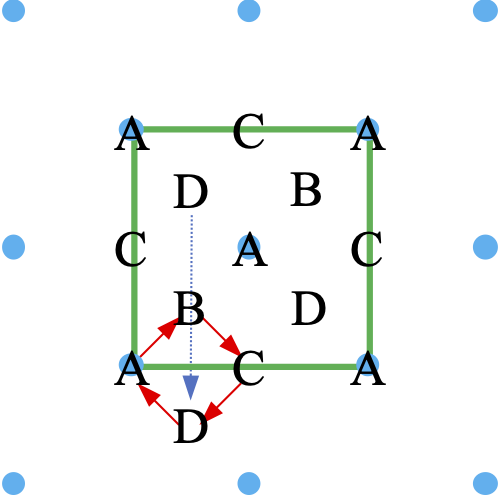
この隣接する層の関係は、ダイヤモンド構造に特有の”d-映進”(鏡映操作(c軸に垂直な面とする)の後、a-b面内の2軸に対して(1/4, 1/4,0)だけ平行移動)という対称操作で重なるものであり、逆に言えば隣接する層は平行移動だけでは重ならない。これは構成原子の共有結合に方向性が存在しているためである。このため、格子点に配置するダイヤモンド構造の基本要素としては、第1層の原子と第2層の原子をペアにして考えるのが通常である。このd-映進面は出来上がったダイヤモンド構造の中にも存在している。また、層状成長を念頭に置いて層に垂直なc軸方向からみた場合のユニットセル内のサイトを図2-8のように定義すると、図2-7に示したa-b面内の移動は、図2-6の構造が積層が進むにつれて1層ごとにA→B→C→D→A→という順序で繰り返されると表現できる。この結果、ダイヤモンド構造では図2-8図で赤矢印で表される4角形の中心に4回らせん軸が出現する。また、層内の2回回転軸と4回回映軸が2層の積層で相互に重なり、結果として2回回転軸の性格が維持される(4回回映の対称操作を2回繰り返すと2回回転の操作となる)。
基本的にダイヤモンド構造では、要素構造を構成する原子の”結合手”の向きが上層に対して確定しており(正4面体の重心から頂点への方向)、上下の層のa-b面内での相対位置は厳格に決まってしまうが、Aサイト、Cサイトに位置する層(以下”α構造”)とBサイト、Dサイトに位置する層(以下”β構造”)は鏡映関係にあって一方の平行移動だけでは他方を構成できないことに留意する必要がある。
さて、ダイヤモンド構造では原子1と原子2が同じものであるため、極めて対称性の高い結晶が実現するが、原子1と原子2が異なる(即ち、閃亜鉛鉱構造)とどうなるであろうか。もともと同一原子種からなる層の積み重ねであったものが、異なる原子種からなる層の交互の積み重ねになる。Si結晶とGaAs結晶で言えば、Si-Si-Si-Si-と言う積み重ねが、Ga-As-Ga-As-になる状況である。α構造とβ構造はもともと鏡面対称関係にあったがその違いに加えて原子種の違いが加わる。この状況を層の対称性の観点から言い換えれば、α構造とβ構造は鏡映関係にあって層群の対称操作によって重なりうるものであったのが、α構造とβ構造を構成する原子種が異なるとこの鏡映対称性(厳密に言えばd-映進対称性)が失われたことになる。
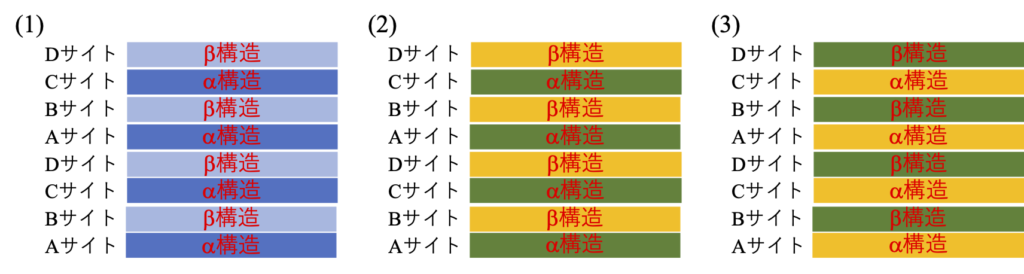
上記で述べたダイヤモンド構造と閃亜鉛鉱型構造の積層状態の違いを図2-9に模式的に示す。ダイヤモンド構造において層間の面を鏡面としてd-映進操作を行っても同じものとなるが、閃亜鉛鉱型構造では同じとならず(2), (3)の間で移り変わる。サイトと構造の対応(各サイトにα構造とβ構造のどちらがあるか)はどれも同一であるが、個々の層の原子種の違いが元素半導体と化合物半導体の大きな差違となっている。
このような違いを前提に、2つのドメインが合体する状況を考えてみると、ダイヤモンド構造の場合にはドメインの層構造は(1)の1種しかあり得ないが、閃亜鉛鉱構造では図2-9の(2), (3)の2種類のドメインがあり得る。この2種のように合体するドメイン間で層構造が異なれば、合体するドメイン間で対応する層内の原子種が異なり、境界には欠陥が発生する。この様子を図2-10に示す。この境界では”結合手”の方向は維持されるが、本来あるべきGa-AsではなくGa-Ga、或いはAs-Asの結合が出来ることになる。また、本来のGa-As結合を作ろうとすればサイトと構造の対応が両ドメインで食い違うことになり(図2-10(4)の様なケースであり、α構造にGaが来るのかAsがくるのかが問題)、いずれにしても欠陥の発生は避けられなくなる。
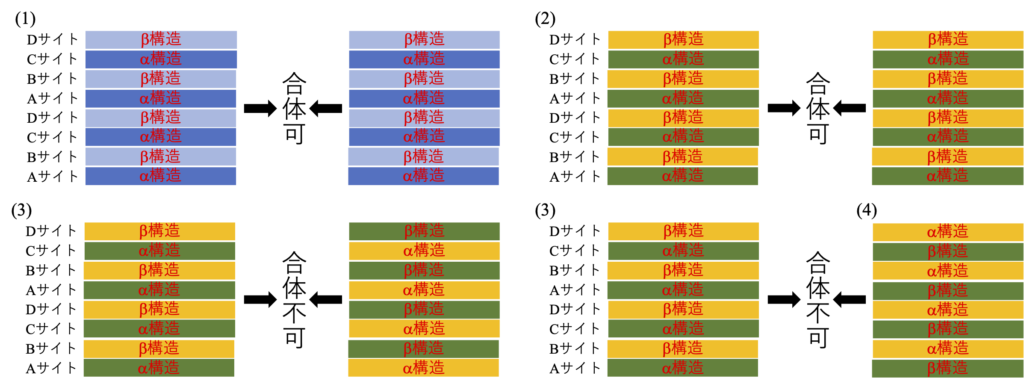
上記の様にして想定される欠陥発生は、実際のエピタキシャル成長においてはGaAs/Siや3C-SiC/Siなど元素半導体(001)面基板上に化合物半導体を成長させる際に基板面に単原子層ステップが存在する時に、しばしば観察される現象である。図2-11にその模式図を示すが、両ドメインは相互にアンチフェーズ領域、その境界はアンチフェーズ境界と称されている。
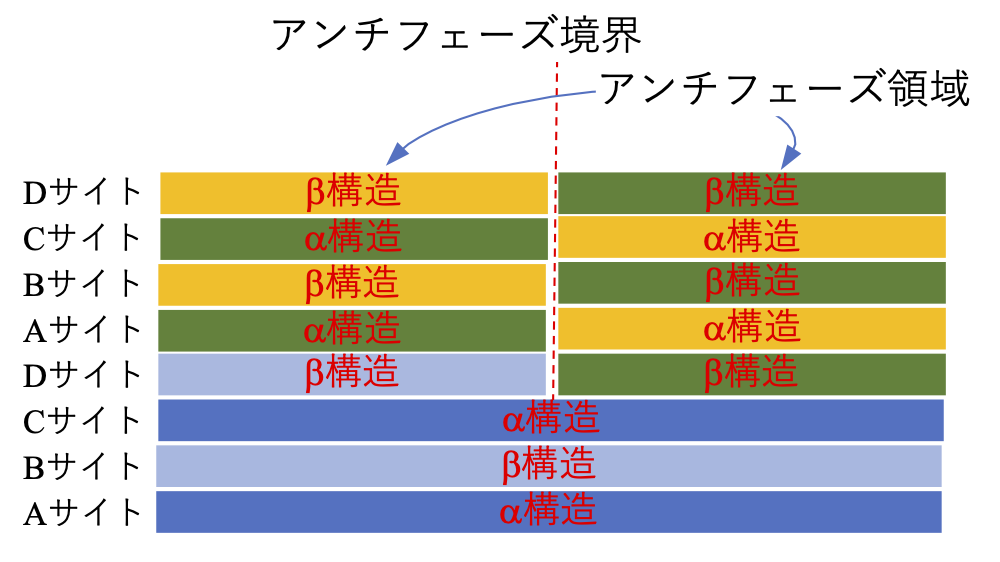
では、実際の半導体エピタキシャル成長において、どのようにすればアンチフェーズ領域の発生をなくせるであろうか。マクロなスケールで基板面全面にわたって原子レベルで上記のようなフラットな面を用意することは事実上不可能である。多かれ少なかれ原子レベルのステップが発生するが、重要なポイントは原子層ステップがあっても、単原子層ステップではなく、2原子層ステップを実現することである。図2-7中で原子の”結合手”が 赤矢印で示されているが、成長の最表面において結合手は未だ結合していない”ダングリングボンド”の状態にある。図2-12に示すように、単原子層ステップでは隣接するドメイン間で最表面のダングリングボンドの向きが90˚異なることになり、その上の成長層間でアンチフェーズ境界が発生する。2原子層ステップであれば、隣接ドメイン間でダングリングボンドの向きが同じになり、アンチフェーズ境界は発生しない。従って実用的な成長技術としては原子層ステップが発生するマクロスケールの表面において、ダングリングボンドの向きの違いを検出できること、並びにステップ発生を制御して2原子層ステップを実現する手法が必要となる。実際、前者に関してはin-situ電子線回折等4)で、後者に関してはオフアングルの角度と向きの適正化を行った上での真空中高温熱処理5)やエレクトロマイグレーション6)等で実現できることが既に報告されている。

今回は、対称性の観点から各種半導体結晶の特徴と関連性を概説し、対称性の違いによる欠陥発生の実例をFCCベースの立方晶結晶に対して考察した。次回はHCPベースの六方晶及び三方晶結晶を対象にして同様の議論を行いたい。
参考文献
- 中澤日出樹・末光眞希・真下正夫: 表面科学 Vol. 24, No. 7, pp.429-433 (2003).
- T. Sakamoto and G. Hashiguchi: Jpn. J. Appl. Phys. 25, L78 (1986).
- Y. Enta, T. Horie, N. Miyamoto, Y. Takakuwa, H. Sakamoto and H. Kato: Surf. Sci. 313, L797 (1994).






