1.はじめに
近年、半導体テクノロジーの重要性が再認識されてきたが、半導体テクノロジーのベースとして、素材としての半導体結晶作成技術は欠くことのできない基幹技術である。「半導体」というと一般的感覚としては半導体デバイスチップを指し示す昨今の状況のもと、今や余り意識されていないかもしれないが、半導体チップのパフォーマンスを十分に引き出すためには、半導体結晶としてのクオリティを高めることが極めて重要である。半導体デバイスは光デバイスにしても電子デバイスにしても、半導体材料の「結晶」の特性を前提にデバイス物理が構築され、その「結晶」としての特性をフルに活用することで、半導体デバイスチップとしての機能を実現している。原子レベルで言うところの「結晶」とは、決まった単位構造(ユニットセルと呼ばれる)が空間的に規則正しく配列した(難しい言い方をすれば、並進対称性をもった)固体を意味するが、半導体結晶の場合、その特性は結晶内部の規則性に大きく影響される。言い換えると、規則性を損なう各種の結晶欠陥をなくしてその完全性を高めることが、半導体結晶には求められる。従って、そのような完全結晶を実現する半導体結晶作成技術が最先端技術としての半導体テクノロジーの根幹をなすと言っても過言ではない。実用的な数インチサイズの大型結晶を想定した場合、そのサイズ全体にわたって完全結晶(ユニットセルの並進対称性が全域にわたって維持されている)であることが究極の目標となるが、その作成過程でミクロサイズの結晶粒が合体することがしばしば起こる。その際に先に述べた「規則正しく配列する」を実現させる究極の技術が、高品質半導体結晶をめざす結晶工学のゴールであろう。しかし、実際の結晶成長では結晶粒の境界で並進対称性(六面体の姿勢を変えない平行移動だけで近隣の六面体と重ねられるか)が維持できずに結晶欠陥が発生する、或いは結晶欠陥の発生が原因で並進が崩れるなどの現象が起こる。結晶中の欠陥は、成長が進むにつれて伝搬し最終的な表面にまで達することもざらにある。その結果、それらの半導体結晶から作製された半導体デバイスチップの性能、特に初期性能のみならず長期信頼性に関する性能の毀損に繋がる事例がまま見受けられる。
半導体テクノロジーの変遷を半導体結晶の観点から歴史的に振り返ってみると、ゲルマニウム(Ge)に始まりシリコン(Si)テクノロジーが大きく発展したことは広く知られているが、Si結晶に関しては現状ほぼ完全結晶に近いものが実現されるに至っている。そしてその高品質大型結晶を活用した各種のSi-大規模集積回路(LSI)が現在の半導体テクノロジーの主役となっている。一方、材料特性からSiでは性能向上に困難が伴う光デバイスや高周波応用に向けて、ガリウム砒素(GaAs)を代表とするIII-V族化合物半導体の開発が進み、Si半導体に続いて実用化が達成された。その後、短波長光デバイスやパワー応用の要求が高まり、そのための半導体材料として窒化ガリウム(GaN)や炭化ケイ素(SiC)等のワイドギャップ半導体に注目が集まった。その結果、これらの材料を用いた半導体デバイスも実現するに至っている。更にパワー応用分野の新規開拓として、今や酸化ガリウム(Ga2O3)、窒化アルミニウム(AlN)やダイヤモンド半導体の開発が着々と進んでいるのが現状である。
ここで、結晶の観点から上記経過で登場した半導体材料を見直してみると、いくつか興味深い点が見受けられる。最初のGeやSiはいわゆる元素半導体であり、結晶構造的にはダイヤモンド構造を持つ結晶である。続いて登場したGaAs等のIII-V族化合物半導体は二元化合物であるが、構造的にはSi等に類似の閃亜鉛鉱型の結晶である。これらの結晶は対称性が高い立方晶系の結晶であるが、続いて登場したGaNやSiCはウルツ鉱型を主体とする六方晶系の結晶となる。更にその後登場したGa2O3は一見それ以前のものとは大きく異なる三方晶系のコランダム構造、或いは単斜晶系の結晶である。
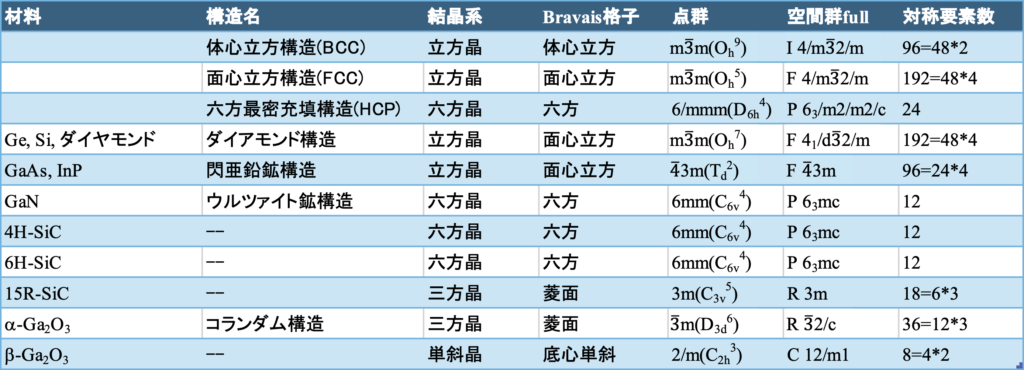
これらの半導体体材料の結晶構造を表1-1に示す(詳細は後述)が、シンプルなものからかなり複雑な構造を取るものまで存在している。ここで、大雑把なイメージとして、結晶系に特有のユニットセル形状を象徴する多数の平行六面体(簡単のため、以後六面体と称する)がバラバラにあって、それらを一つの箱に収納する作業を想像してほしい(図1-1参照)。多数の六面体を無秩序に箱に入れても、なかなかきれいには並ばない。しかし、箱を揺らしてみるなど、外界から刺激を与えれば完全ではないかもしれないがそれなりに順序正しく並ぶ、それもサイコロのような立方体であればより簡単に並んでいく(逆に言えばいびつな六面体であればより並びにくい)現象は何となく実感できるのではないだろうか。また、図1-2に示すように、六面体が規則正しく並んでいるところ(結晶)に、その六面体を取り出して回転することによって姿勢を変えた上で配置することを考えてみよう。立方体であれば、特定の軸の周りに90˚回転しても頂点は相互に入れ替わっているもののその空間座標軸(図中のx, y, z軸)に対する全体としての姿勢は変わらず、結晶にそのままの姿勢で取り込める。ところが、一般的な六面体では同じ回転操作を施してもそのまま結晶に取り込む事は出来ない。このような状況を鑑みると、六面体が立方体のような高い対称性(イメージ的に言えば、8頂点に区別がない等)をもっていれば、より規則正しく並び易いのではないかという思いが頭をよぎる。
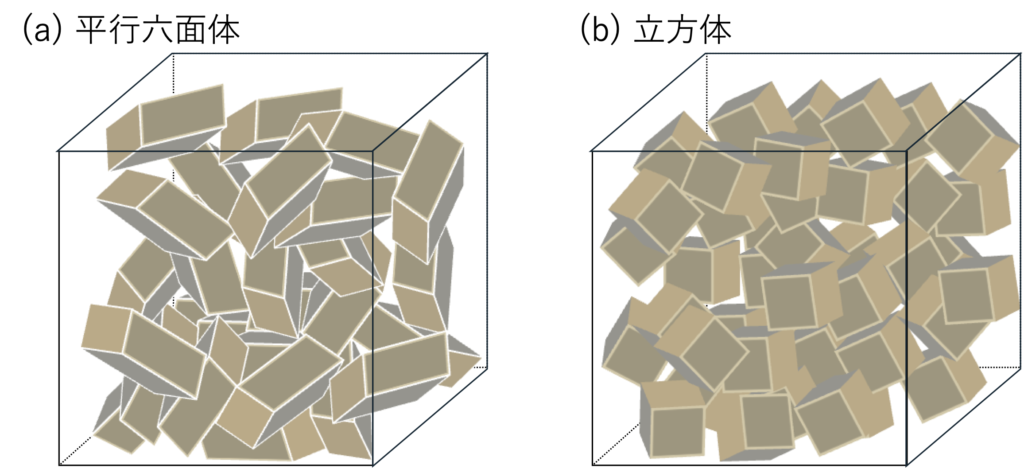
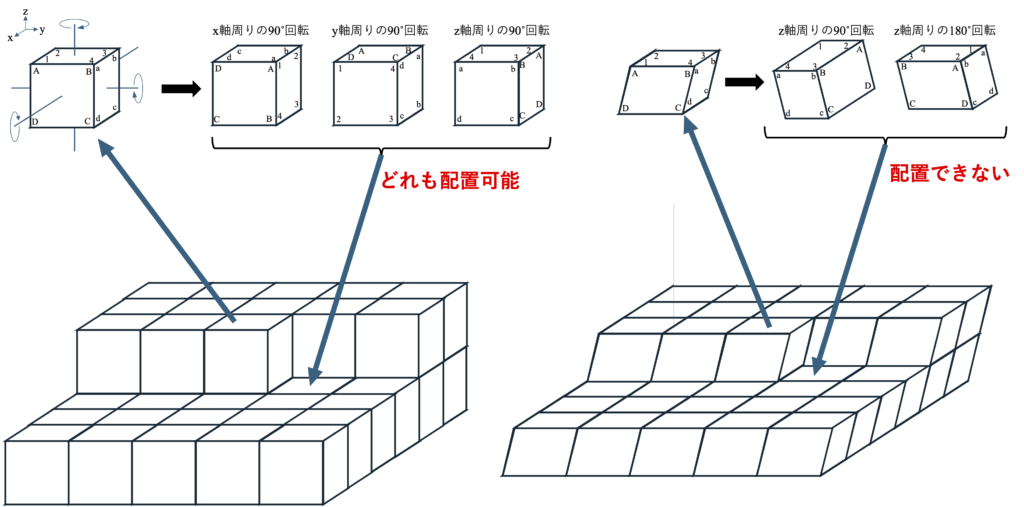
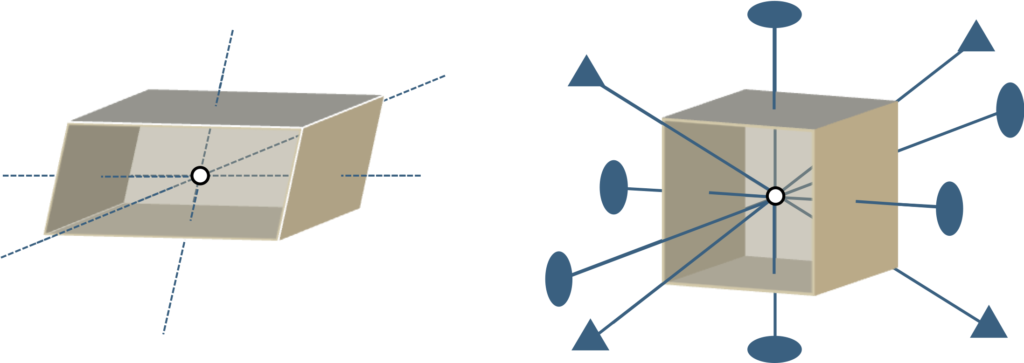
図1-3に六面体と立方体の対称要素の一部を示すが、例えば回転に対して立方体は4回対称軸や3回対称軸を持つ一方、六面体では反転中心しか存在しない。言い換えれば、空間的な自由度に対して立方体の方が同じ姿勢を保ち易く、ひいては規則正しく配列し易いのではないか。即ち、結晶のユニットセルの対称性が高いほど3次元空間を並進対称性を保ってうまく埋めつくせる(無欠陥な完全結晶を意味する)のではないかと期待される。各材料の結晶は、ユニットセルの対称性を表現する”Bravais格子”とその格子点に配置される”基本要素”の対称性を反映した点群、更にはBravais格子と点群の組み合わせから導かれる”空間群”と呼ばれる対称要素の集団によって特徴づけられる。まずは格子で表現されるユニットセルの対称性が空間を埋め尽くすのに都合が良いかどうか(並進群の問題?)、さらには基本構造の対称性並びに化学結合の方向性等(点群の問題?)がユニットセルの配置にどう影響するか。それぞれの空間群が持つ対称要素の数が対称性の良し悪しの1つの指標となるかもしれない。本記事ではこれらの半導体材料間の共通性や相違点を特に結晶の対称性(平行移動や回転操作で結晶全体が重なるかどうか)、並びにエピタキシャル成長を軸とした結晶成長に伴う結晶欠陥発生の観点から独自の視点も含めて図も多用しながらわかりやすく比較してみたい。見方を変えれば3次元空間中で積み木細工をしていくような感覚の議論であり、気楽に読み進んで頂ければと思う。第2回では立方晶、第3回では六方晶、第4回ではその他の結晶を取り上げて最後にまとめとする予定である。
尚、結晶学に特有の用語や基本的概念の説明は、煩雑になるため本文中では詳しく述べていないが、末尾にAppendix(1, 2, 3)として記載したので詳細はそちらか参考文献1,2)を参照頂ければと思う。また、現象の完全な理解にはエネルギー的な観点が必要かもしれないが、この記事の対象としては形態的な結晶学的議論までに留めていることをご容赦いただきたい。






