アイシーソルーションズ, LLP

　本稿では、パワーMOSFETのドリフト層設計の最適化について考える。おおかたのパワー半導体デバイスの解説では、p⁺n^–接合のn^–ドリフト層側に広がる空乏層の電界分布の図を使って、最大電界と空乏層濃度と耐圧の関係を説明している。n^–ドリフト層は十分厚く、空乏層がn^–ドリフト層内に止まることを前提としたモデルである。ところが実際のパワー半導体デバイスでは、空乏層が必ずしもn^–ドリフト層内に止まらない設計が多用されているのだ。

　パワーMOSFETの話に入る前に、空乏層がn^–ドリフト層内に止まらない具体例としてIGBTを見ておこう。図1にIGBTの代表的な構造を示す。左から、(a)パンチスルー型（PT型）、(b)ノンパンチスルー型（NPT型）および　(3)フィールドストップ型（FS型）の3種類である。

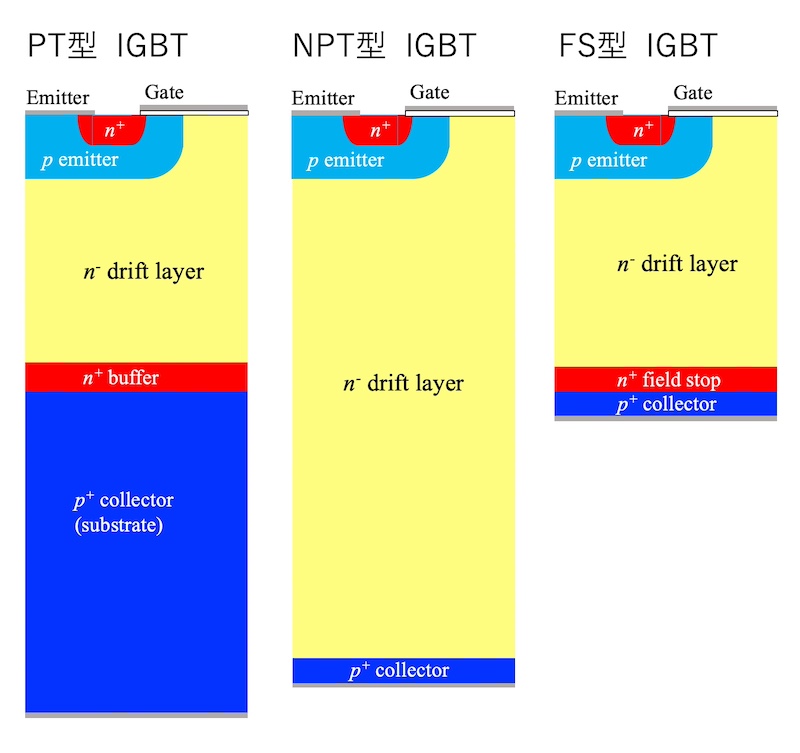
　これらの構造を区別するのに「パンチスルー」というキーワードが出てくる。IGBTがOFFで、エミッタ コレクタ間に電源電圧がかかると、逆バイアスになるp型のエミッタとn型のドリフト層のpn接合に電圧がかかり、空乏層が低濃度のn^–ドリフト層に伸びる。もし空乏層がn^–ドリフト層を越えて高濃度p型のコレクタにまで達すると、pコレクタとn^–ドリフト層のpn接合に順方向バイアスがかかり、pコレクタから正孔注入が始まりOFFを保てなくなる。エミッタ接合から延びる空乏層がコレクタ接合まで突き抜けるという意味で、この現象をパンチスルーと呼ぶ。パンチスルーを起こすと、高電圧がかかった状態で大電流が流れ、最悪IGBTの破壊に至る。

　パンチスルーが起きては困るので、n^–ドリフト層を十分厚くしたのがノンパンチスルー（NPT）型である。エミッタpn接合位置を原点として、x軸を深さ、y軸を電界強度としてグラフを描くと、図2左側に示すように、電界は、エミッタpn接合面位置で最大値、空乏層端で0になる深さの一次関数になる。NPT型では、エミッタ接合に設計上の最大電界強度Emaxがかかっても空乏層端がコレクタ接合まで達しないように、n^–ドリフト層の厚さを決めている。

　n^–ドリフト層とpコレクタとの間に高濃度n⁺層を挟んだ構造をパンチスルー（PT）型と呼ぶ。図2右側のように、空乏層がn^–ドリフト層を越えて伸びても、n⁺層内で急速に電界が減少して空乏層はn⁺層内で止まる。PT型は、エミッタ接合に設計上の最大電界強度Emaxをかけても、空乏層がn⁺層を越えてコレクタ接合まで届かないように設計されている。PT型と呼ばれても、上述のパンチスルー現象を起こすわけではないことに注意してほしい。n⁺層で電界を受け止めるという意味で、フィールドストップ（FS）型と呼ぶ方が誤解がないだろう¹。以下では、FS型と呼ぶことにする。

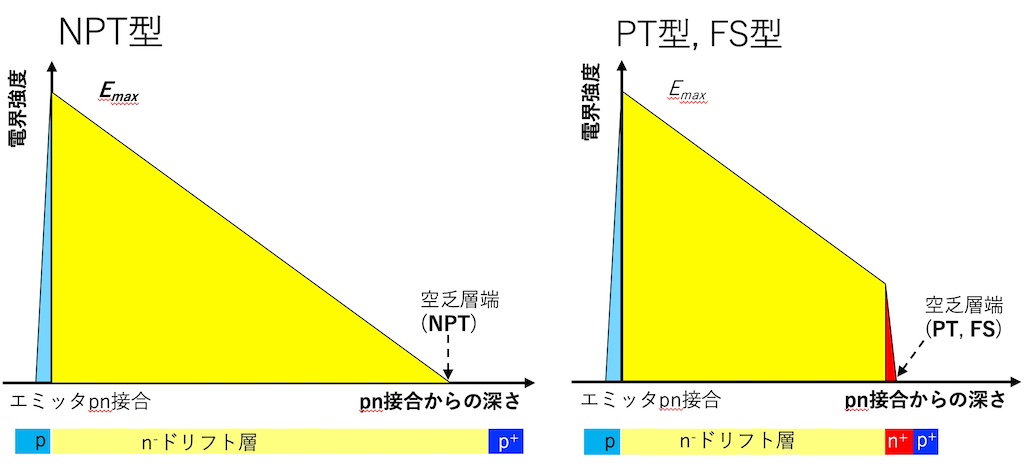
　図2のような電界分布を持つパワーデバイスの耐圧を復習しよう。図2左のNPT型では、n^–ドリフト層の電界分布の直線の傾き（絶対値）がドナー濃度に相当し、空乏層の電界強度を深さ方向に積分した黄色い直角三角形の面積が、pn接合にかかる電圧、つまりこのデバイスの耐圧になる。FS型では、図2右のように、空乏層の電界強度分布が台形状になり、黄色い台形の面積が耐圧になる。

　図2の左右を見比べると、NPT型の直角三角形の空乏層端側の一部を切り取るとFS型の台形になる。FS型の台形の面積はNPT型の直角三角形の面積よりも小さくなる。単純にNPT型のドリフト層を薄くしてFS型にすると耐圧が下がってしまうのだ。

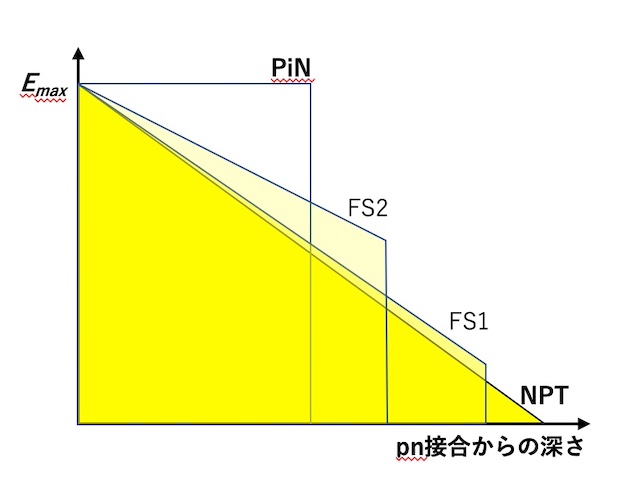
　FS型でNPT型と同じ耐圧を得るには、NPT型から切り取った直角三角形の面積分だけFS型の台形の面積を増加させれば良い。pn接合側の台形の長辺はEmaxで決まっていて、これ以上伸ばせないので、図3のように、空乏層端側の短辺を伸ばすことになる。それを実現するには、n^–ドリフト層内の電界の傾きを小さく、つまり、n^–ドリフト層のドナー濃度を下げる必要がある。濃度を0まで下げた極限では、ドリフト層の電界が一定になり、p層とn層で真性半導体層を挟んだPiNダイオードになる。PiN構造では図3のように、切り取った直角三角形と付加される直角三角形が合同なので、ドリフト層厚さは、NPT型の半分になる。

　バイポーラ素子のIGBTがONの時は、pコレクタからn^–ドリフト層へ正孔が注入されて、n^–ドリフト層の伝導度変調を起こす。ON抵抗はn^–ドリフト層に大量に注入された少数キャリア濃度で決まり、n^–ドリフト層濃度のON抵抗への影響は小さい。IGBTでは、FS型にするとNPT型と同じ耐圧を保ちつつn^–ドリフト層を薄くできる。導通時には、FS型の薄いn^–ドリフト層に蓄積される少数キャリアの総量がNPT型よりも少なくなり、電流遮断が速くなる。すなわちスイッチング損失の減少にもつながる。IGBTでは、FSを採用してめでたしめでたし。現在IGBTの主流はFS型である。

ーーーーーーーーーーーーーーーー

　前置きが長くなった。ここから本論である。パワーMOSFETには、NPT型とFS型どちらが向いているのだろう。パワーMOSFETは、高濃度n型基板の上にn⁺バッファー層、n^–ドリフト層を順に成長したエピウェハの上にMOSトランジスタを形成する。IGBTとは異なりドレイン側にpn接合が存在しない。MOSFETのソースpn接合にEmaxがかかった時に、空乏層がn^–ドリフト層内で止まればNPT型、n⁺層まで達すればFS型になる。MOSFETの耐圧の決まり方はIGBTと変わらない。一方、伝導度変調がないユニポーラ素子のMOSFETでは、n^–ドリフト層の濃度と厚さが、直接ON抵抗に効いてくる。

　図3のNPTとPiNの両極端を見ると、NPTでは、n^–ドリフト層濃度が最も高く抵抗率が最小になる一方、その厚さは最大になる。逆に、n^–ドリフト層濃度を薄くした極限のPiN構造では、抵抗が無限大になって導通しなくなる²。MOSFETではn^–ドリフト層の濃度と厚さがON抵抗に対してトレードオフの関係にあるのだ。

　一番ドリフト抵抗が小さいのはNPTなのか、それともNPTとPiNの間に最適点があるのか、簡単な計算で求めてみよう。n^–ドリフト層の電界分布を図4のようにモデル化する。pn接合の最大電界強度を 1 に、NPTの空乏層幅を 1 に正規化する。こう定義すると、直角二等辺三角形の面積 1/2 が耐圧に相当し、直線の傾きの絶対値 1 がNPTの場合のn^–ドリフト層濃度に相当する。

　ドリフト層の抵抗は、（n^–ドリフト層厚さ）と（n^–ドリフト層の抵抗率）の積なので、n^–ドリフト層の移動度がキャリア濃度によらず一定と仮定すれば、（n^–ドリフト層厚さ）と（直線の傾き(絶対値)の逆数）の積に比例する。ここでは、NPTのドリフト層抵抗を次のように正規化することとする。

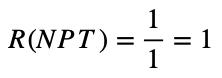
　pn接合から深さ x にn⁺層を設けたFS構造を考える。NPTで x = 1、PiNで x = 1/2 になるので、 x をこの範囲で考える。n^–ドリフト層末端位置 x の電界強度を y とすると、NPT構造とFS構造が同耐圧になるには、FS構造の台形面積が 1/2 であれば良いから、

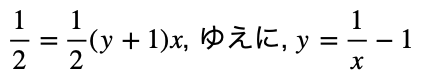
　FS構造の直線の傾き(絶対値)は、

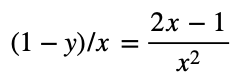
　ゆえに、n^–ドリフト層厚 x のFS構造のドリフト層抵抗が次式のように求まる。

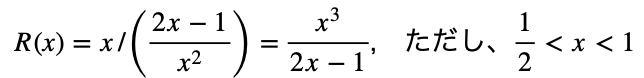
　図5に、ドリフト層抵抗 R(x) とその逆数（導電率）の計算値を示す。

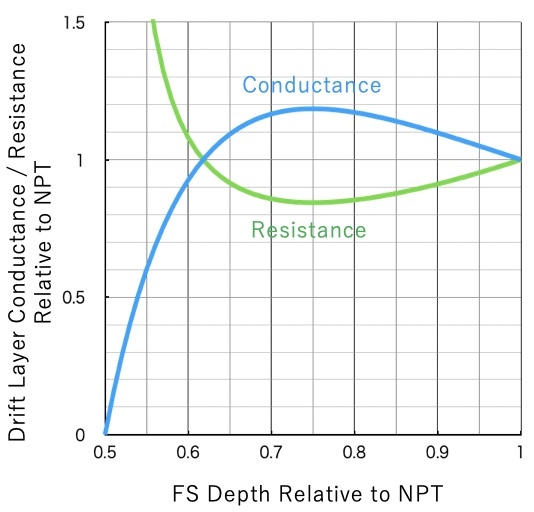
　NPT構造 ( x = 1 ) から耐圧を維持しながら、FS構造を採用してn^–ドリフト層を薄くしていくと、R(x)が 1 から徐々に減少し、比較的緩やかな底を過ぎて、PiN構造 ( x = 0.5 ) に近づくと急速に発散する（導電率が0へ）。MOSFETでも、NPTよりもややFS気味にした方がドリフト層抵抗が小さくなるのだ。R(x)最小の条件を求めると、

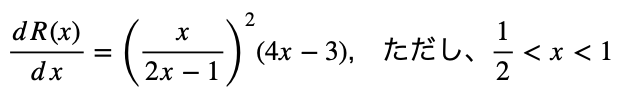
　ゆえに、

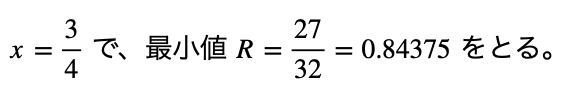
　FSにすることで、同耐圧のNPTよりもドリフト層抵抗が最大15%ほど改善される³。この最適条件での電界分布を図6に示す。

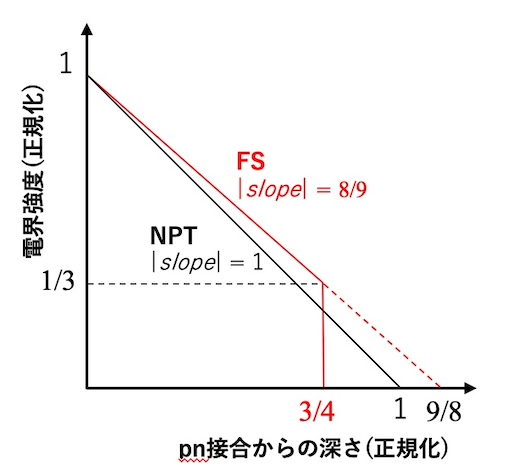
図6 を使って色々な場合のMOSFETドリフト層設計を考えてみよう。

例1　ある耐圧でドリフト層抵抗が最小になるMOSFETのドリフト層を設計する。一番オーソドックスな課題である。

(1) 所望の耐圧が得られるNPT構造を求める。

• 半導体材料に合わせてEmaxを設定する。直角三角形の高さが決まる。
• 直角三角形の面積が所望の耐圧になるように、底辺の空乏層幅を決める。
• 直角三角形の斜辺の傾きから、n^–ドリフト層濃度が決まる

(2) 求めたNPT構造をドリフト層抵抗が最小になるFS構造に変換する。

• 　n^–ドリフト層厚さを、NPT設計値の3/4倍に。
• 　n^–ドリフト層濃度を、NPT設計値の8/9倍に。

例2　耐圧が 10kV を越えるようなSiC MOSFETでは、濃度 10¹⁴cm^-3 台で厚さ 100μm 以上のn^–ドリフト層が必要になる。このような低濃度かつ厚膜のエピタキシャル成長は難しく、再現性が良くないため、n^–ドリフト層濃度が規格から外れたエピウェハが数多くできてしまう。もったいないので有効活用を考えたい。

n^–ドリフト層濃度が規格より濃い場合は、

• 成長したn^–ドリフト層濃度で直角三角形高さEmaxのNPT空乏層幅を求める。
• NPT空乏層幅を2/3倍⁴にしたFS構造の耐圧を台形の面積から求める。当初設計値より低くなるが、そのエピ基板を使ったMOSFETの耐圧とドリフト層抵抗の最適組み合わせになる。
• その耐圧でも良ければ、求めたFS構造の厚みにエピタキシャル成長層を削り、MOSFETを作製する。

n^–ドリフト層濃度が規格より薄い場合は、上記の方法で耐圧とドリフト層抵抗の最適組み合わせを求めると耐圧が当初設計値より高くなる。活性部の耐圧が、周辺耐圧部やパッケージの設計耐圧を越えても意味がないので。あくまでも設計耐圧を実現することにする。

• 成長したn^–ドリフト層濃度で、耐圧が規格値になるFS構造の厚さを求める。
• そのFS構造でのドリフト層抵抗を求める。当初設計値よりは高くなる。
• そのドリフト層抵抗でも良ければ、求めたFS構造の厚みにエピタキシャル成長層を削り、MOSFETを作製する。

ーーーーーーーーーーーーーーーー

　パワーMOSFETでも、n^–ドリフト層をNPTよりはややFS気味にした方が、ON抵抗が下がることを簡単な解析で示した。パワーMOSFETを設計している人は経験的に知っていることで、すでにどこかで解説されていることと思うが、筆者が上記例2にあるような問題意識を持ったときに、代表的なパワー半導体の教科書⁵をあたってみたところ、NPT構造やFS構造のn^–ドリフト層濃度と耐圧の関係は丁寧に書かれているが、それをMOSFETのドリフト層抵抗と結びつけた説明が見当たらなかった。仕方なく、鉛筆と紙を持ちだして、手計算したメモがこの解説の元になっている。

（坂本邦博）

1. PT型とFS型の区別には歴史的経緯がある。IGBT開発の初期に、p⁺基板上にn⁺層、n^–ドリフト層を順にエピタキシャル成長で作製したPT型が登場した。その後、低濃度のウェハを薄膜化してn^–ドリフト層に使い、表面にMOSFET構造を形成した後に、裏面にp⁺コレクタを形成する技術が開発された。この時点では、パンチスルーするほどウェハを薄くできなかったので、NPT型と呼ばれた。さらにウェハを薄くする技術開発が進み、裏面にパンチスルー防止n⁺層を加えた構造が登場すると、すでにあったPT型と区別するため、FS型と名付けられた。IGBTの導通時には、FS型とPT型ではドリフト層の伝導機構が異なり、両者の区別に意味があるのだが、本解説で論じる耐圧設計に限れば、PT型とFS型に違いはない。 ↩︎
2. ここでは、均一ドープのn-ドリフト層を考えているが、スーパージャンクション構造のドリフト層を持つSJ-MOSFETでは、ドリフト層のp型コラムとn型コラムのチャージバランスを取ることで、空乏化した時にPiN構造と同じ長方形の電界分布をとりつつ、導通時は低ON抵抗を実現する。スーパージャンクションはパワーMOSFETの理想型であるが、その製造は均一ドープと比べて格段に難しい。 ↩︎
3. 半導体の絶縁破壊電界から決まる最大電界強度Emaxと、n^–ドリフト層のキャリア移動度が一定と仮定して計算した。実際の半導体では、絶縁破壊電界やキャリア移動度が不純物濃度に依存することが知られている。不純物濃度が桁で変わるような場合は濃度依存性の考慮が必要だが、図6を見ると、NPTとFS最適解のn^–ドリフト層濃度の違いは12%程にすぎず、一定値と仮定して大きな誤差はない。 ↩︎
4. ドリフト層濃度が決まっているので図6の赤い線を基準に考える。NPT空乏層深さ9/8に対して最適FS深さが3/4なので、(3/4)÷(9/8)=2/3となる ↩︎
5. B.J.Baliga, “Fundamentals of Power Semiconductor Devices”, Springer, New York, 2008. ↩︎