この連載では、昨今世間で議論になる電力エネルギーの過不足に関する話題を取り上げ、kWとkWhの混同に起因する誤解を紹介してきた。その前提として、電力というものは基本的に貯蔵することが出来ず(大規模電力システムに対応できるような実用的電力貯蔵装置は現時点では未だ存在しない)、作った電気は瞬時に使ってしまわなければならないと言う命題が存在している。
ところで、電力エネルギーの過不足、即ち発電された電力と消費される電力の間のアンバランスが起こると電力システムの中で実際には何が起こって、何が困るのであろうか。世の中の解説書やネット情報を探してみても、送電網が維持できないとか発電所が停止してブラックアウトが起こるとか、結果としての抽象的な説明はされている。ブラックアウト、即ち大停電がどのようなものか、その例は本連載の(2)で紹介しているので、詳しくはそちらを参照いただければと思うが、具体的に電力システムの中で、どのような現象が起こってブラックアウトに至るのか、わかりやすく解説されたものは極めて少なく、最終結果を理解したつもりになっても、その過程で多くの「ナゼ」が頭の中でそのまま残っていて、何かモヤモヤした気分でいる方が結構多いのではないかと推察している。そこで本連載の最後として、電力エネルギーの過不足が実際の電力システムの中で何をもたらすのか、独自の視点で考察してみたい。以下は巷の多くの解説とは些か異なるアプローチを取っているが、電力分野の非専門家の独自の考察としてご容赦願いたい。
今回は、議論のアプローチとして、エネルギー保存則、及び交流送電の二つのポイントからの瞬時電力(本連載タイトルの「キロワット」の方)の過不足の議論を行ってみたいと思う。最初に単純化したエネルギーシステムを想定して、トータルの電力エネルギー収支から負荷が増えた際に(発電動力源の運転状態に変化なく、特別な対応処置がなければ)どのような現象が起こるか考察を進める。次いで交流の議論に特有の「位相角」、特に長距離送電の際に重要な指標となる「相差角」の観点から、同様な考察を進めることにする。
まず、電力システムの簡易モデルとして、単一の発電機と単一の負荷を想定しよう。また、物理の大原則であるエネルギー保存則を本議論の出発点として採用しよう。発電機は、同期発電機とし、その動力源は発電機を回す機械的なエネルギーである。実際、火力発電におけるボイラー等からの蒸気や水力発電における水流等も羽根車を回す機械的エネルギーに一旦変換されている。この発電機としての簡易モデルを負荷側の構成と共に図1に示す。
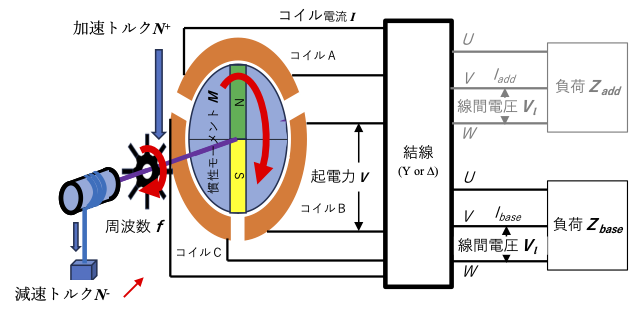
このような系における発電機側を対象としてエネルギー収支を考える場合、機械的エネルギーと電磁的エネルギー双方が含まれるため、定量的扱いが若干複雑になることにご注意願いたい。機械的エネルギーとしては発電機の回転子の回転運動エネルギーと外部動力源が発電機の回転子を回そうとする機械的トルク、電磁的エネルギーとしては電流出力に伴って回転子の回転を抑制しようとする電磁的トルクがあり、それらの間に、エネルギー保存則から次のような式が成立する。ここでは、単位時間当たりの変化(変化率)を考えているため、回転エネルギーに対しては時間微分、トルクに対してはその行う仕事率(角速度との積)を用いて記述している。

(1)
ここで、M:回転子の慣性モーメント、ω:回転子の角速度、
N+:回転子を加速させようとして働く動力源からの機械的トルク
N+ ω = Pm(機械的入力パワー)、
N–:回転子を減速させようとして働く電磁的トルク
N– ω = Pe(電磁的出力パワー)、である。
また、減速トルクの仕事率N– ω は外部負荷に対する仕事率に相当し、
V:送り出される電力の電圧、
I:送り出される電力の電流、
cos θ:送り出される交流電力の力率
として
の関係になる。ここで、N– はIに比例していることに注意頂きたい。
N– ω = I・V cos θ
(2)
ここで、Vとω の間に電磁気学から導かれる関係が存在するが、それを簡約して比例関係V = α ω(起電力は回転子の角速度に比例)と置くことが出来る。また、負荷に対するオームの法則から負荷の総インピーダンス(直流的に考えるなら抵抗値)をZとして、V = Z・ Iとなる。まとめると、独立変数としての時間tと5個の未知数V, I, N+, N–, ω に対して関係式が4個あることになり、未知数を消去していくと以下の様な回転子の角速度 ω (t)、及び機械的トルクN+に対する一階微分方程式が導かれる(kは比例定数)。
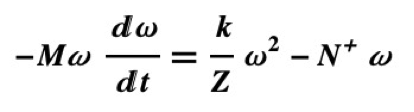
(3)
さて、この微分方程式をよく見て頂きたいが、N+は動力源の運転状態に関するパラメータとして扱い、トルク(N+)を一定とするかパワー(N+ω)を一定とするかで(3)式のN+ω 項の扱いが異なるため、解の形が若干違ってくる。今回は、この微分方程式の解法の詳細については踏み込まないことにするが、電力の発生と消費のバランスが取れている状態では、左辺のdω /dt が零となる定常状態になり、その時のZ, N+, ω の値をZ0, N+0, ω0 (Z0 はZの初期状態での値)とする。
ここで、初期状態から負荷としてのZがΔZだけ変動する場合を考える。図1で言えば、初期状態がインピーダンスZbase ( = Z0 )である負荷のみのところに、インピーダンスZaddをもつ新たな負荷が加わった状態である。このとき電圧V、電流I、角速度w は、共に同じ時定数(Mに反比例)を持って新しい定常値に収束していくことが導かれる。ご注意頂きたいのは、発電機側のIは負荷側のIbaseとIaddの和であること、負荷Zaddは通常並列接続となるため、Zaddが加わった後の総インピーダンスZはZ= (Z0・Zadd) / (Z0 + Zadd)となって減少することである。先に定義したΔZはΔZ = Z0 – Zとなる。負荷側の総インピーダンスZとその変動ΔZに基づく発電機側の電流 I(t)、電圧V(t)の過渡応答を一例として図2に示すが、
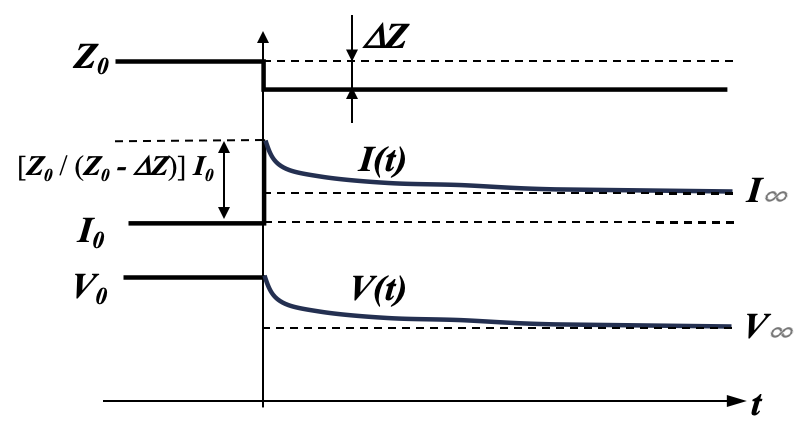
負荷側で新たに電力機器が動作してトータルとしてのZがΔZだけ減少した場合、Vが収束していく新しい定常値V∞ は
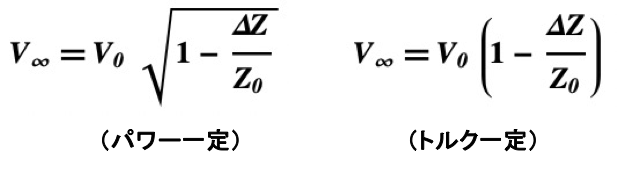
(4)
となることが導かれる。いずれの場合でもV∞ はV0 より小さくなり、ω も同様な挙動を示す。逆にI∞ はI0 より大きくなる。また、図2に示される減衰カーブの時定数は発電機の回転子慣性モーメントMに反比例しており、Mが大きければ大きい程、電圧Vの急激な変動を抑制できることになる。これが「慣性力」として知られ、太陽光パネルなどには見られない機械的発電機の大きなメリットである。(逆に、零から発電機を起動する際にも時間がかかることになるのだが。)
ここまでは、負荷変動後の過渡応答を解析的に考察してきたが、上記の新たな定常状態についての考察結果を改めて考え直してみると、発電機出力電力の式 P = V・I cosθ と負荷側のオームの法則 V = Z・I から当たり前に導かれるとも言える。Pを一定とすると、負荷が増えた場合にはその一定であるPを負荷全体でシェアすることになり、当然VとIはオームの法則に従って積を一定に保った初期状態とは異なる値となる。即ちIが増加した分、Vが減少する。但し、負荷変動直後にはIのみが増えてVは変化せず、その後I、V共に新たな定常値に減少しており、その結果Pは一時的に増えている時間帯が存在するが、その増加分は回転子の運動エネルギーの減少で相殺されている事になる。
世の中で電力系統に対する暗黙の要求は、電圧と周波数の安定性である。通常、負荷側にある電力機器はその前提であらかじめ決められている定格周波数や定格電圧からの逸脱がおこると、満足な動作が出来なくなる。また電流に関しても、線間電圧Vlが減少することによって個々の機器はVl / (個々の機器のインピーダンスZeach )で決まる電流しか得られず、動作に必要な電流供給を十分に受けることが出来ない状態となる。
以上のような状況を、図1の構成でオームの法則とN– ω = I・V cosθ (N– ∝ I )、式(1)の関係を考慮して「風が吹けば桶屋が儲かる」風の連鎖的な言い方でイメージ的に表現すれば、
負荷Zadd が発生 ⇒ 負荷(線)電流 Iadd が発生 ⇒ 発電機のコイル電流 I の増加 ⇒ 発電機の回転に対する抵抗として働くトルクN– が増大 ⇒ 角速度 ω、周波数 f の低下 ⇒ 起電力Vの低下 ⇒ (線間)電圧Vl の低下 ⇒ Ibase が減少、 Ibase + Iadd は Ibase 初期値( = I0 )より増加
の様なものであろうか。このような状況は負荷側の個々の電力機器としては定格性能を満たせない事を意味する。また、発電機側としては定格に比べて過電流になることを意味し、機器の損傷に繋がる恐れがある。また、上記とは逆に負荷が減少した(Zが増加)場合、全て逆のことが起こるが、その場合も個々の電力機器側では過電圧と過電流、発電機側では回転子の角速度(周波数)上昇による機器損傷に至る可能性が出てくる。いずれの場合も、電力システムとしてはゆゆしき事態である。







コメントを残す