はじめに
REDG効果によってn–ドリフト層中に存在する基底面転位から、積層欠陥がどのように生成するのかを連載(8)以降で考察しています。成長した積層欠陥の形状を調べると、どのような素性の基底面転位が積層欠陥の原因かは推察できます。基底面転位の素性がわかれば、プロセスの改良可能かもしれません。連載(7)で、界面転位と貫通刃状転位の交差によってn–ドリフト層中に短い基底面転位が形成されることを言及しました。連載(10)のこの回は、これらの交差によって発生する短い基底面転位からどのような形状の積層欠陥が生成するかを考察します。
(D-2) 界面転位と貫通転位との交差
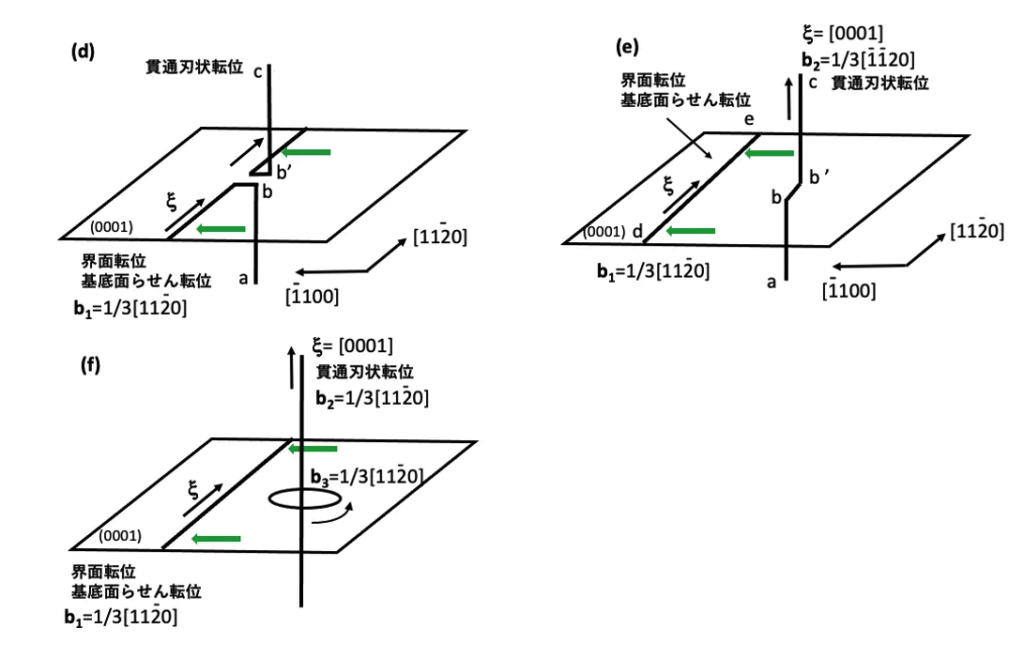
界面転位が形成され、それらが活動している際に貫通刃状転位と交差し、貫通刃状転位に折れ曲がりを発生させたり、貫通転位の周囲にリング状の基底面転位を残したりすることは連載(7)で述べました。貫通刃状転位に折れ曲がりが発生する点では、連載(9)の(D-1) エピ層中に発生した貫通刃状転位の折れ曲がりと同じ事なのですが、この折れ曲がりは界面転位がのっているすべり面と同じすべり面で発生するので、話は少し複雑になります。また、界面転位がばら撒いた多数のU字状転位から生成する積層欠陥と、貫通刃状転位の折れ曲がりから生成する積層欠陥の間で積層欠陥ドメイン境界の形成や、合体などが推察されます。
貫通刃状転位と界面転位の交差によって生成される基底面転位部分はとても短く、1バーガース・ベクトル分の長さ、つまり1単位胞の長さです。この部分から積層欠陥の成長は可能です。さらに、エピ層成長後のデバイスプロセス中に何らかの応力が作用すると、短い基底面転位が移動して張り出します。基底面転位が長くなり、効率良く積層欠陥が成長すると考えられます。今回は、エピ層成長後のデバイスプロセス中に、何らかの応力によって基底面転位が張り出した場合も考察します。
基底面転位の張り出しを考慮する理由は、もう一つあります。貫通刃状転位と界面転位との交差で発生する短い基底面転位の場合、基底面転位の向きはξ=[1120]に固定されています。しかしながら、エピ層成長プロセスの後のデバイスプロセス中に何らかの応力が加わると、基底面転位の向きはξ=[1120]以外のさまざまな方向を向くように張り出します。このため、基底面転位の張り出した場合も考察する必要があるかもしれません。
n–ドリフト層中に存在する他の基底面転位の場合も、デバイスプロセス中に何らかの応力が加わると基底面転位が動いて張り出したりします。しかし、すでに議論したn–ドリフト層中の他の基底面転位の場合、さまざまな方向を向く場合もすでに考察しています。そのため張り出しによる基底面転位の向きの変化については特に考察していません。今回の貫通刃状転位と界面転位の交差の場合には、短い基底面転位の張り出しによる基底面転位の向きの変化も考察しておくことも必要かと考えられます。
まず最初にb=1/3[1120]のL字状界面転位と貫通刃状転位との交差について考察します。この交差は四面体A’層またはC’層のすべり面で発生します。その次にb=1/3[1120]の逆L字状界面転位と貫通刃状転位との交差について考察します。この交差は四面体A層またはB層のすべり面で発生します。
(D-2) a: b=1/3[1120]の貫通刃状転位とL字状界面転位の交差
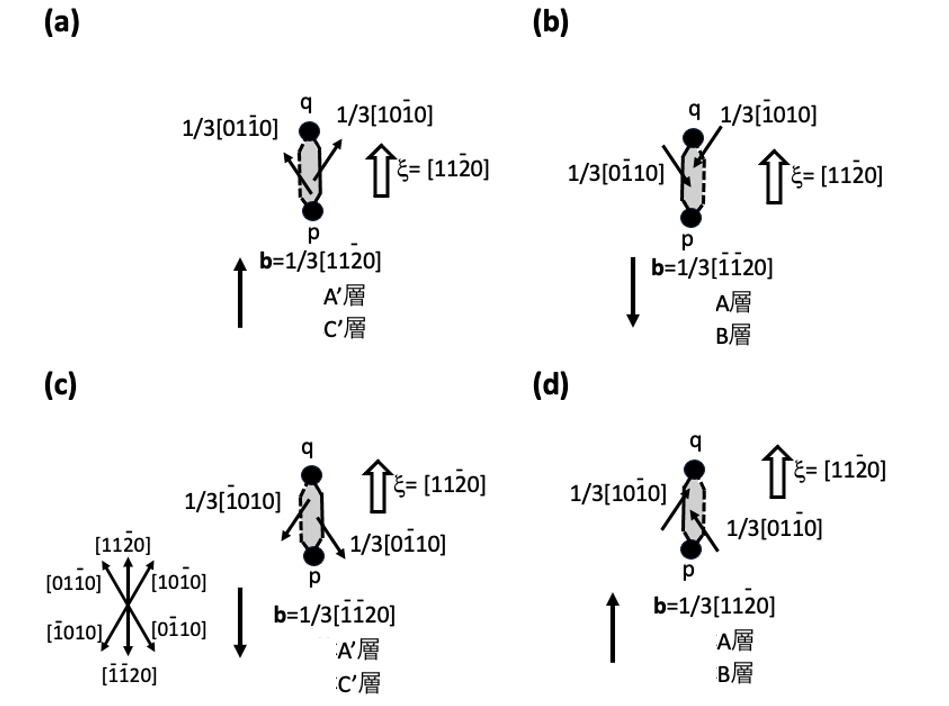
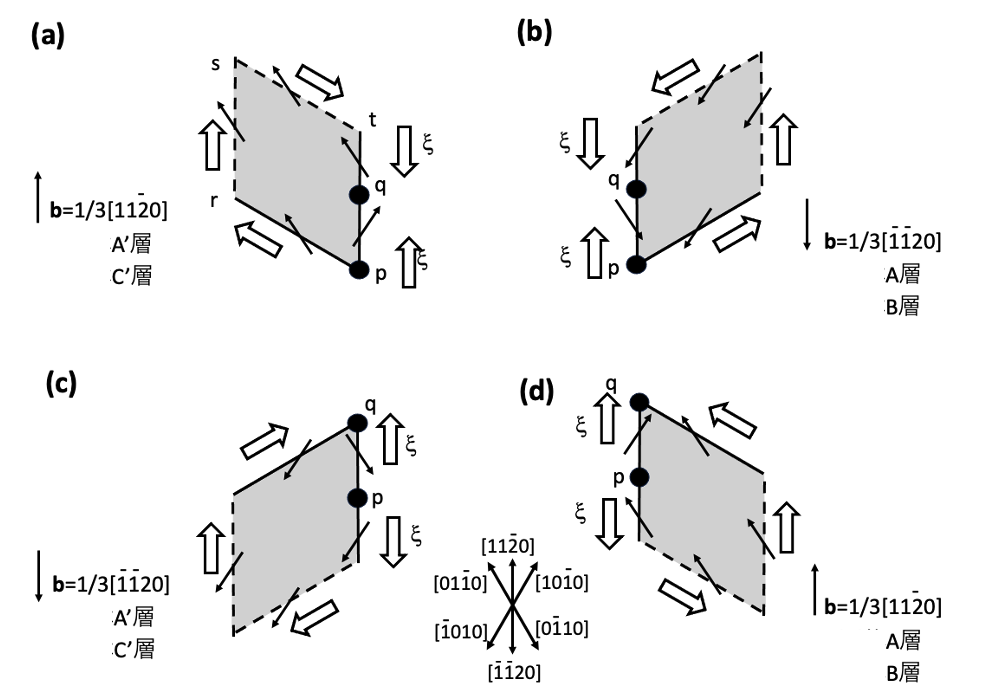
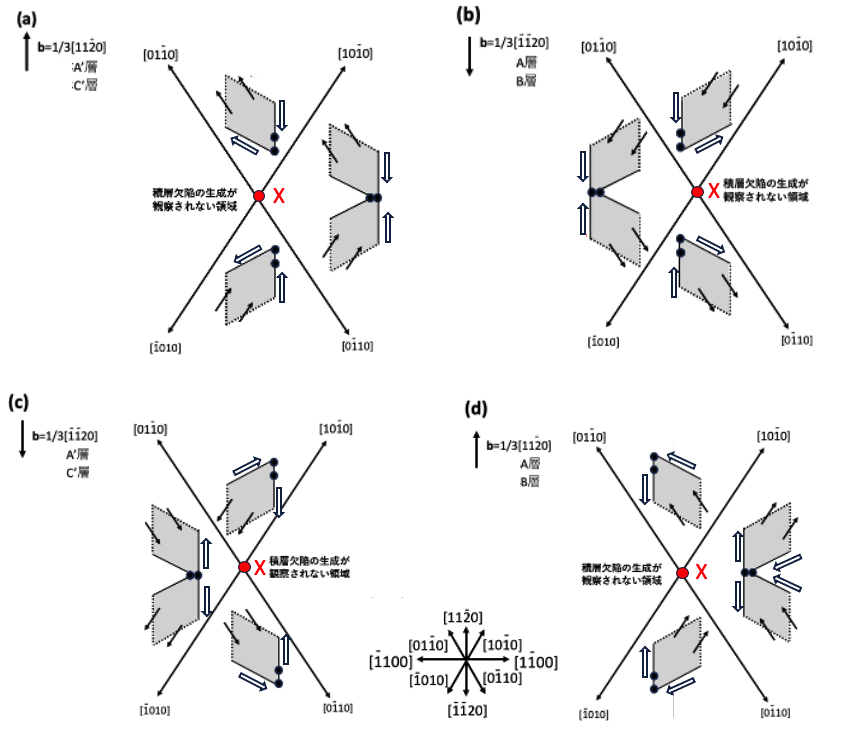
b=1/3[1120]のL字状界面転位とb=1/3[1120]の貫通刃状転位が交差した際に形成される短いb=1/3[1120]の基底面転位から生成する積層欠陥の成長を考察します。この交差のプロセスは図7-3(d),7-3(e)に示しています。図10-1 (a) は交差後に発生したξ=[1120]、b=1/3[1120]の短い基底面転位opを示しています。この交差は四面体A’層またはC’層のすべり面で発生します。この図は図4-2(c)そのものです。成長する積層欠陥の形状は図4-3(c)や、図5-6(c)での11時から1時方向の場合で示されています。この短い基底面転位から単体の菱形積層欠陥が[1010]方向に向かって成長することは推察されます。
図10-1 (a)の短い基底面転位は、赤い破線で示したb=1/3[1010]のSiコア部分転位と黒い線で示したb=1/3[0110]のCコア部分転位から成り立っています。連載(1)で説明していますが、1000℃以下の温度では4H-SiCの結晶に何らかの応力が加わるとSiコア部分転位のみがすべり面に沿って動きます。Cコア部分転位は動きません。1000℃以上の温度ではCコア部分転位も動くことは知られていて、エピ層成長プロセス後のデバイスプロセス中に何らかの応力がこの転位に加わると1000℃以上の高温ではSiコア部分転位、Cコア部分転位の両方が動きます。図10-1 (b) は1000℃以上の温度でのデバイスプロセス中で、何らかの応力がウエハに加わり、その結果、Siコア基底面部分転位、Cコア基底面部分転位の両方が動き、基底面転位opが左方向、つまり[1100]方向、に張り出しqrの位置に移動した状態を示しています。
図10-1 (b)の状態が形成された後のREDG効果での積層欠陥の成長を考察します。張り出したループの内側は、ループ内側の部分転位のSiコア基底面部分転位が動き、積層欠陥によって埋められます。ループの外側のSiコア基底面部分転位はこのまま成長を続け結局、図10-1 (b’)のような形状の単体の菱形形状の積層欠陥が成長します。
図10-1 (b’) は、また室温でのデバイスプロセス中に何らかの応力が加わり図10-1 (a) の状態からSiコア部分転位のみが左方向に張り出しqrの位置に移動した状態をも、示しています。この状態が出現すると、REDG効果により図10-1 (b’) は、このままこの形状の積層欠陥が大きき成長します。つまり、REDG効果により、単体菱形積層欠陥が[1010]方向に向かって成長することが考えられます。つまり、図10-1 (a)の短い基底面転位が一旦出現すると、高温で応力を受けて図10-1 (b)の状態が形成された場合も、室温で応力を受けてもまた受けなくても、最終的にREDG効果により図10-1 (b’) のような形状の積層欠陥が出現します。
図10-1 (c)は、1000℃以上の温度でのデバイスプロセス時に、何らかの応力が加わった際に、基底面転位opが右方向、つまり[1100]方向、に張り出しq’r’の位置に移動した状態を示しています。(b)のように左方向に基底面転位が移動するのか(c)のように右方向に移動するかは加わる応力の方向に依存します。この張り出しの場合、転位opのCコア部分転位が先に動き、その後にSiコア部分転位が後からついて来る状態です。実際の観察では、通常Siコア部分転位が先に動き、その後にCコア部分転位が後からついて来ることが、エピ層成長時の高温プロセスで観察されます。図10-1 (c)のように、Cコア部分転位が先に動き、後からSiコア部分転位がついて来るような動き方が実際に発生するかは不明ですが、十分な高温ではCコア部分転位が自由に動き回るようになり、Cコア部分転位が先に動き、後からSiコア部分転位がついて来ることは可能だと思われます。ここではそのようなことが可能な場合を想定して考察を進めます。図10-1 (c)のように基底面転位が張り出した場合に、REDG効果によって形成される積層欠陥の形状を図10-1 (c’)に示します。単体の菱形積層欠陥が[0110]方向に向かって成長します。
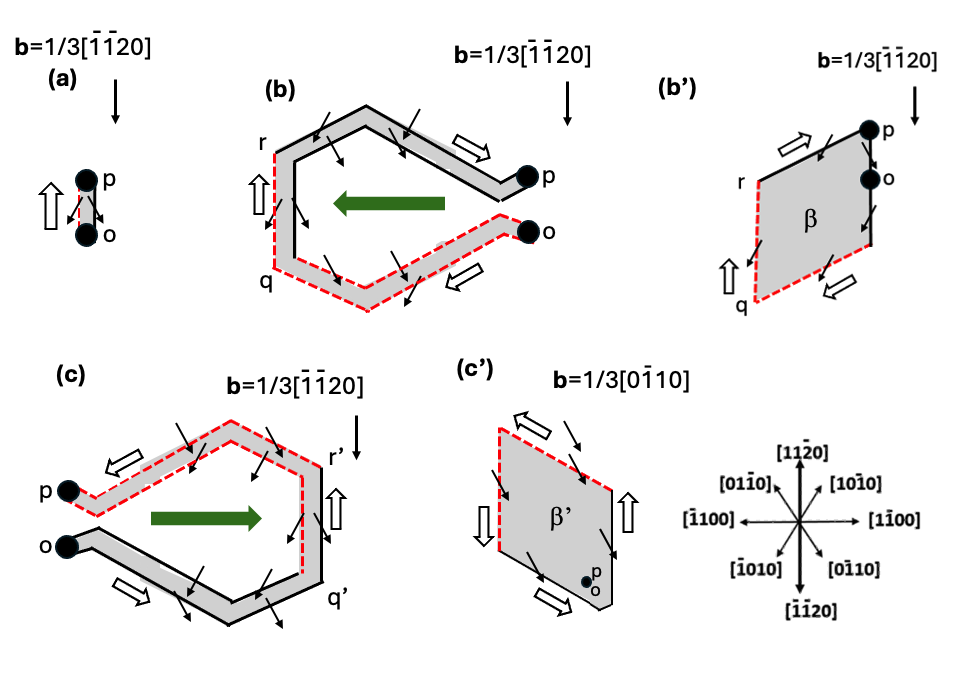
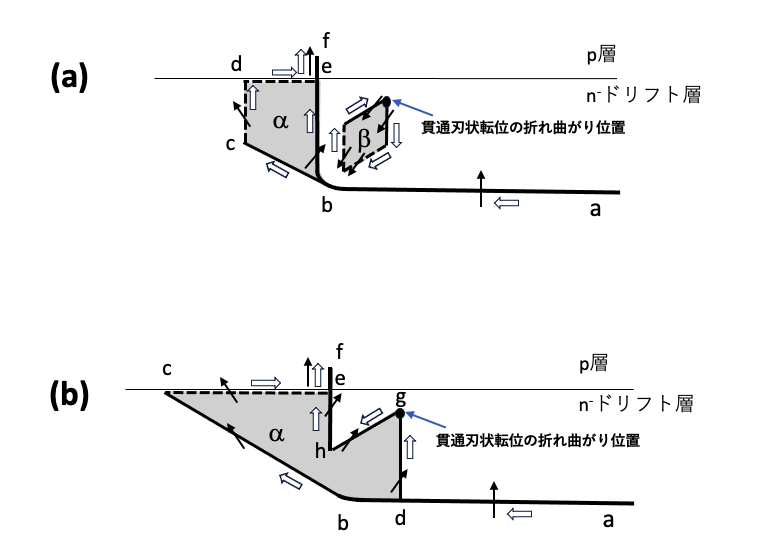
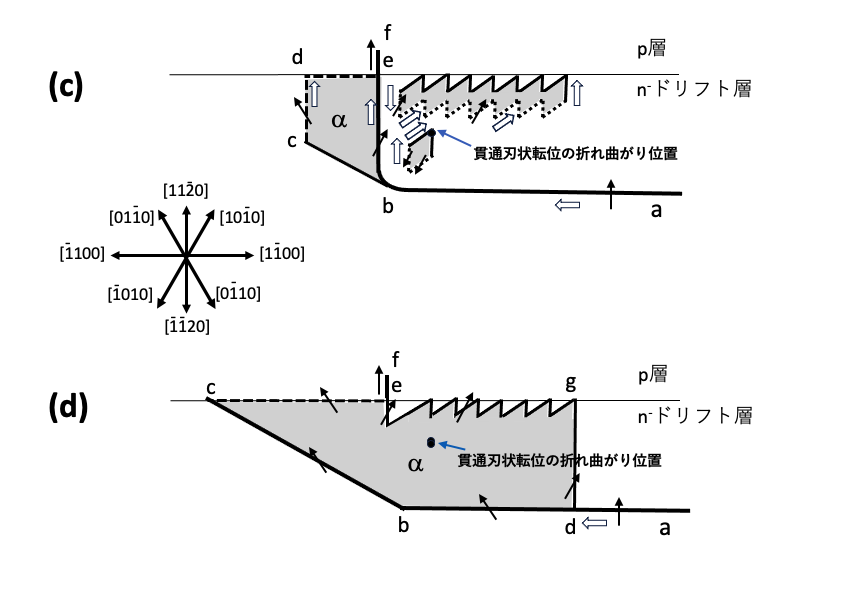
図10-2(a)はb=1/3[1120]の貫通刃状転位折れ曲がり部分の基底面転位から、REDG効果によって積層欠陥βが成長している状態を示します。この積層欠陥βの形状は図10-1(b’)そのものです。図10-2(b)はさらに成長が進み、界面転位から成長した積層欠陥αと積層欠陥βは反応し1枚の積層欠陥αになっています。図10-2(c),(d)はL字状界面転位の表面終端部がばら撒いたU字状の転位が存在している場合を想定しています。U字状転位から生成する積層欠陥とも反応し1枚の積層欠陥αになります。ただし、貫通刃状転位の折れ曲がりによって生じた短い基底面部分転位はそのまま内部に残ります。交差によって発生した短いb=1/3[1120]の基底面転位が図10-1(b),(b’)のような張り出しの場合でも、張り出さない図10-1(a)の場合でも、結局、図10-2(a),(b),(c),(d)の形状の積層欠陥は発生します。
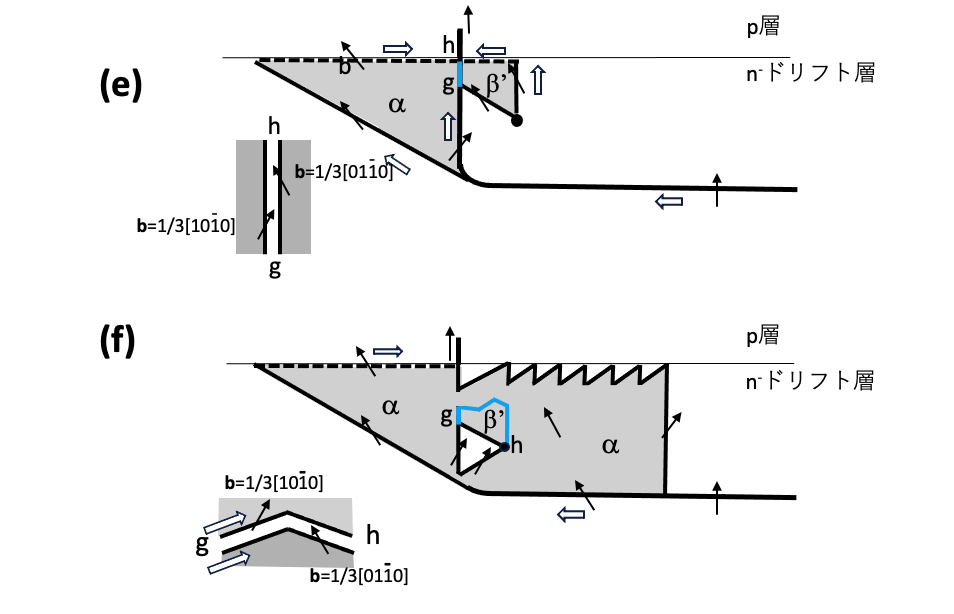
図10-1 (c’)のような積層欠陥β’の発生の場合、最終的に図10-2(e)または(f)のような形状の積層欠陥が現れます。図10-2(e),(f)では、積層欠陥α, β’は合体して一枚の積層欠陥になることはできず、青い線ghで示す積層欠陥のドメイン境界を形成します。図10-2(e),(f)の左下の図は積層欠陥のドメイン境界ghの拡大図を示します。このドメイン境界ghの構造はb=1/3[1120]の基底面転位と見なすことも可能ですが、四面体A’またはC’のすべり面上の基底面転位とは部分転位の配置が逆になっていて、構造が異なっています。また図10-2 (f)の場合、最終的に積層欠陥の中に特徴的な穴が開いています。
(D-2) b: b=1/3[1120]の貫通刃状転位とL字状界面転位の交差
次に、b=1/3[1120]の貫通刃状転位との交差を考察します。この交差により図7-3(f)に示す小さな基底面転位リングの生成を想定します。この基底面転位リングの向きを時計回りに設定すると、バーガース・ベクトルはb=1/3[1120]です。この基底面転位リングからのREDG効果により成長する積層欠陥の形状は、結局、図10-2(a),(b),(c),(d)と同様な状態が出現します。







コメントを残す