アイシーソルーションズ, LLP

(D-1) エピ層中に発生した貫通刃状転位の折れ曲がり

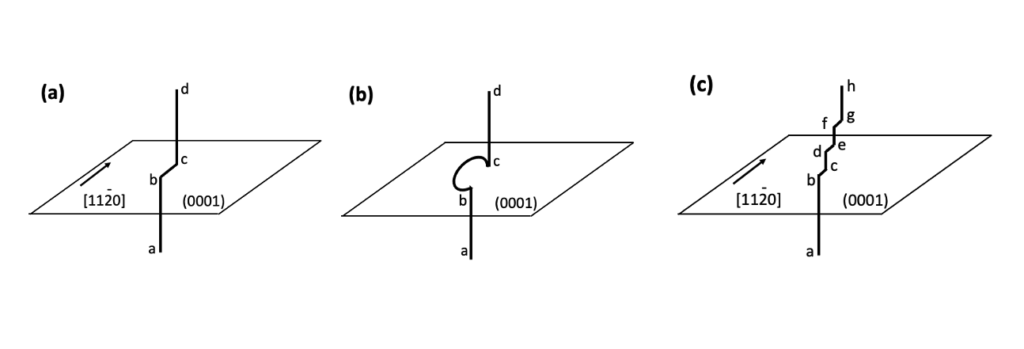
連載 (8)では、(A)基底面転位から貫通刃状転位への変換に際して、エピ層中に入り込んだ基底面転位から生成する積層欠陥の形状について考察しました。これらの積層欠陥は、エピ層/基板界面近傍からの成長でした。エピ層中の貫通刃状転位の折れ曲がりから発生する場合の積層欠陥の形状は、 (A)の場合とは少し雰囲気が異なります。図7-1(a)のモデルで示されている貫通刃状転位が折れ曲がることによって出現する短い基底面転位から生成する積層欠陥の形状や現れ方はすでに、連載(5)の図5-6, 5-7, 5-8で詳細に考察しているので、その結果を参考にすると話は簡単です。

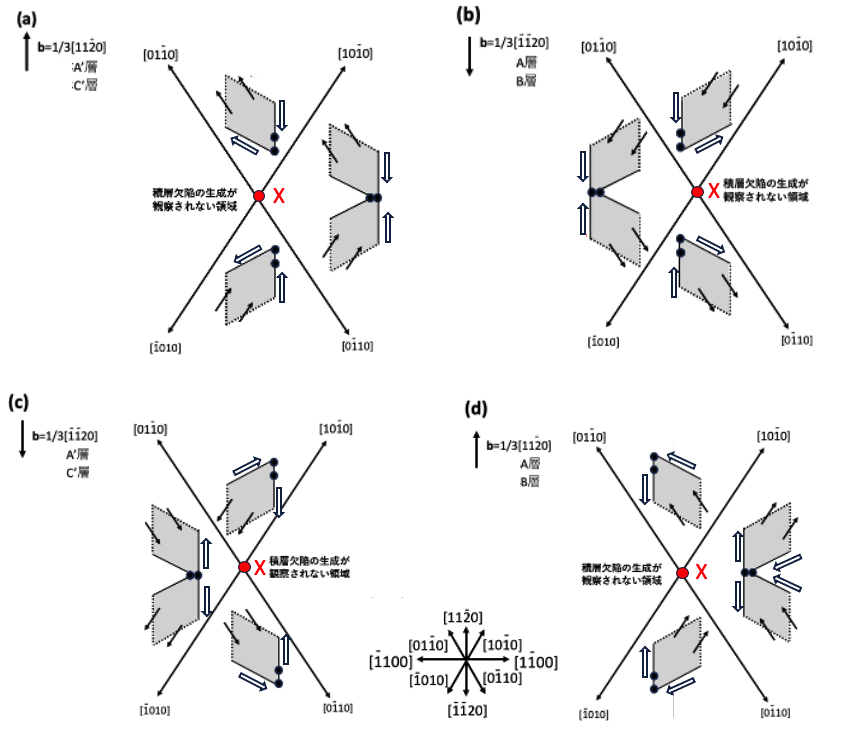
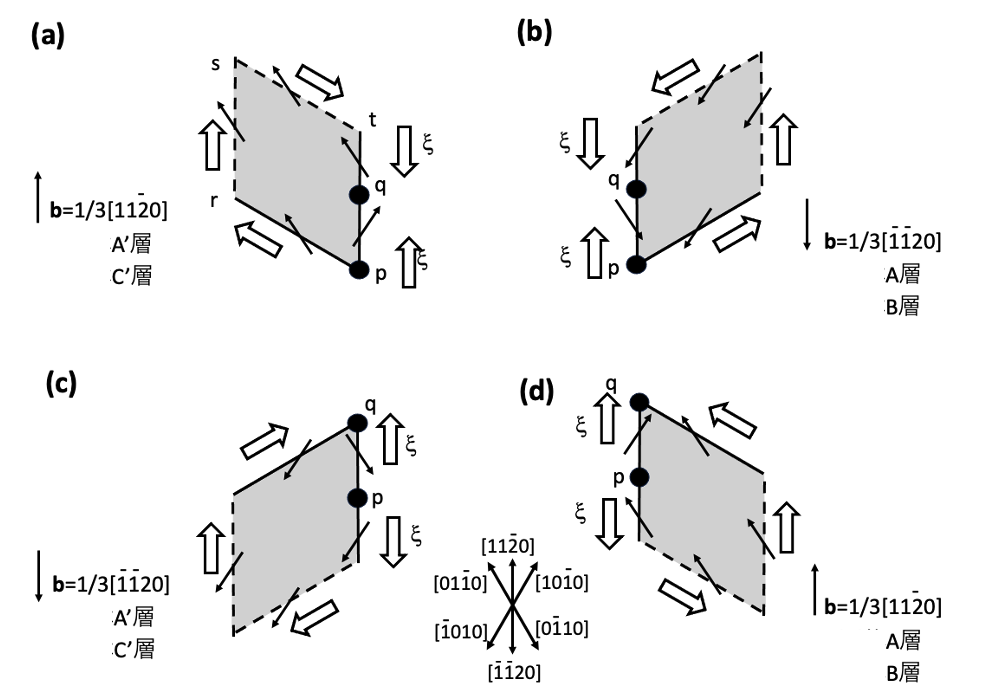
図9-4はb=±1/3[1120]の貫通刃状転位がn^–ドリフト層中で折れ曲がりを形成し、折れ曲がり部から菱形積層欠陥が成長し、成長が飽和した状態の模式図です。積層欠陥の形状は、図4-3(a),(b),(c),(d)や図5-6(a),(b),(c),(d)から簡単に描くことができます。また貫通刃状転位の折れ曲がり位置は、n^–ドリフト層の真ん中の深さの位置を想定して描いています。図9-4では短い折れ曲がりを持つ貫通刃状転位の位置を黒丸で示していて、貫通刃状転位の折れ曲がり位置がp層部に近い場合は発生源の黒丸の位置は図中の上側へシフトします。図9-4(c),(d)の場合、三角形状の積層欠陥は大きくなります。また図9-4(a),(b)の場合、三角形状の積層欠陥は小さくなります。貫通刃状転位の折れ曲がり位置がn⁺層部に近いと、逆に、図9-4(a),(b)の場合、三角形状の積層欠陥は大きくなります。また図9-4(c),(d)の場合、三角形状の積層欠陥は小さくなります。

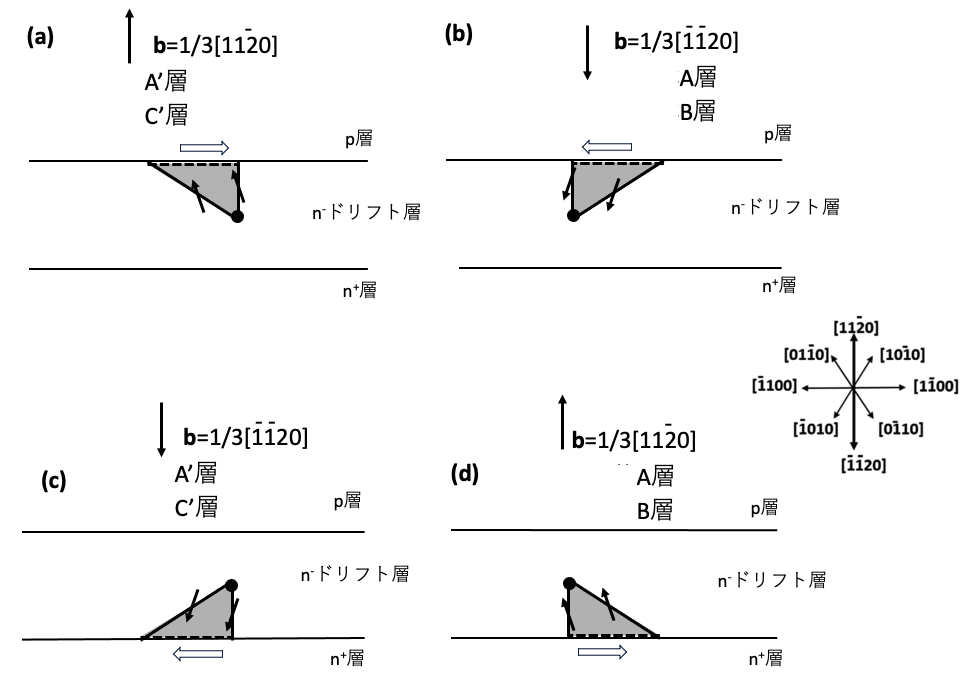
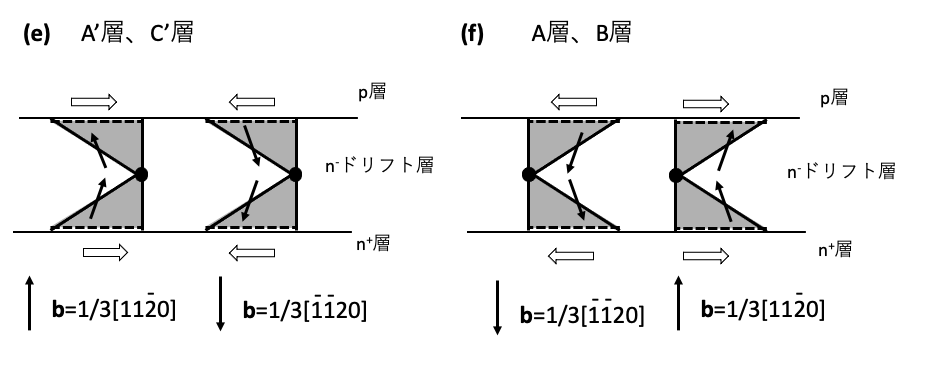
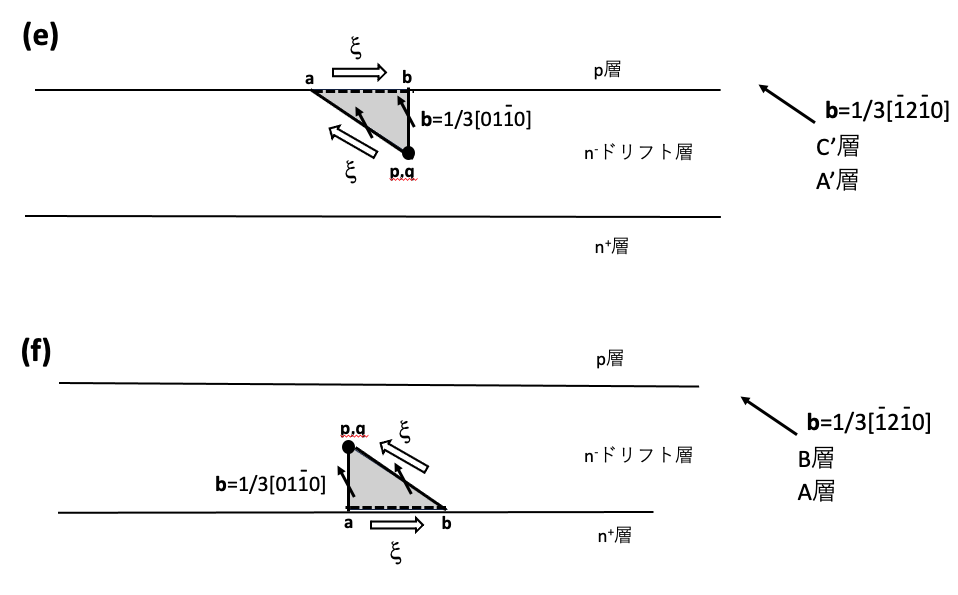
図9-4(a),(b),(c),(d)では折れ曲がった際に形成される基底面転位の向きは11時方向から1時方向の範囲を想定しています。エピ層が成長する際のステップフロー方向が[1120]方向なので、貫通刃状転位が表面モフォロジーに引きずられることを仮定して、折れ曲がって形成される基底面転位の向きを11時方向から1時方向に想定することは適切だと推察されますが、その他の向きの場合の一例を図9-4(e),(f)に示します。図5-6を参考にすると、図9-4(e)はb=1/3[1120]の基底完全面転位がA’層またはC’層に存在し基底面転位の向きが1時から5時の向きの範囲の場合か、あるいはb=1/3[1120]の基底面転位が、A’層かC’層に存在し基底面完全転位の向きが7時から11時の向きの場合です。これらは、図5-6(a),(c)に示されていて容易に理解できると思います。図9-4(f)はb=1/3[1120]の基底面転位がA層かB層にあり、折れ曲がって形成された基底面転位の向きが1時の方向から5時の方向の範囲の場合が想定されます。また、b=1/3[1120]の基底面転位がA層かB層にあり、折れ曲がって形成された基底面転位の向きが7時の方向から11時の方向の範囲の場合が想定されます。これらは図5-6(b),(d)に示されていて容易に理解できると思います。図5-6(a),(d)を見ると、b=1/3[1120]の基底面転位の向きが7時から11時の場合は折れ曲がりが発生してもREDG効果による積層欠陥の湧き出しはないことがわかります。また、図5-6(b),(c)を見ると、b=1/3[1120]の基底面転位の向きが1時から5時の場合は貫通刃状転位に折れ曲がりが発生してもREDG効果による積層欠陥の湧き出しはないことがわかります。

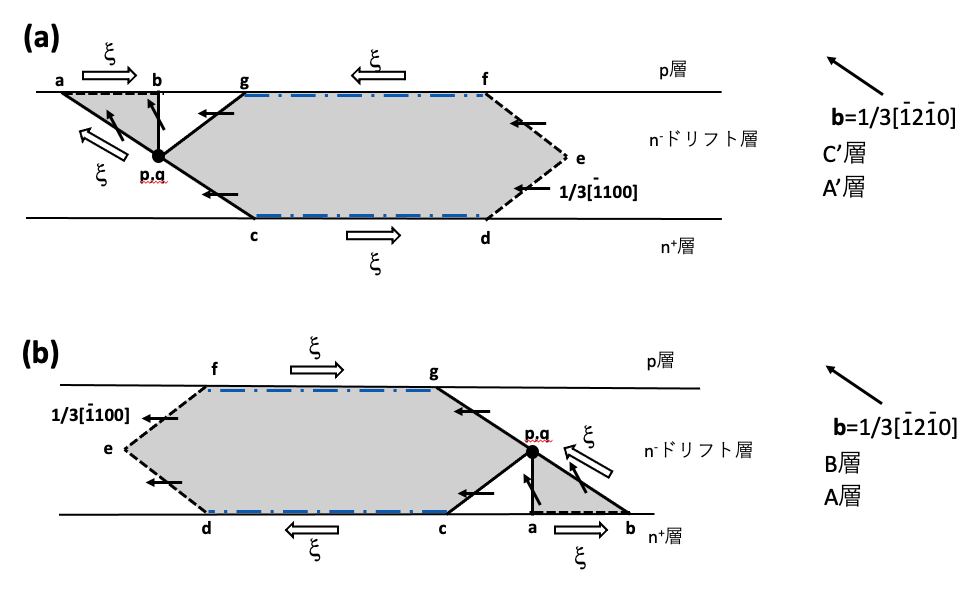
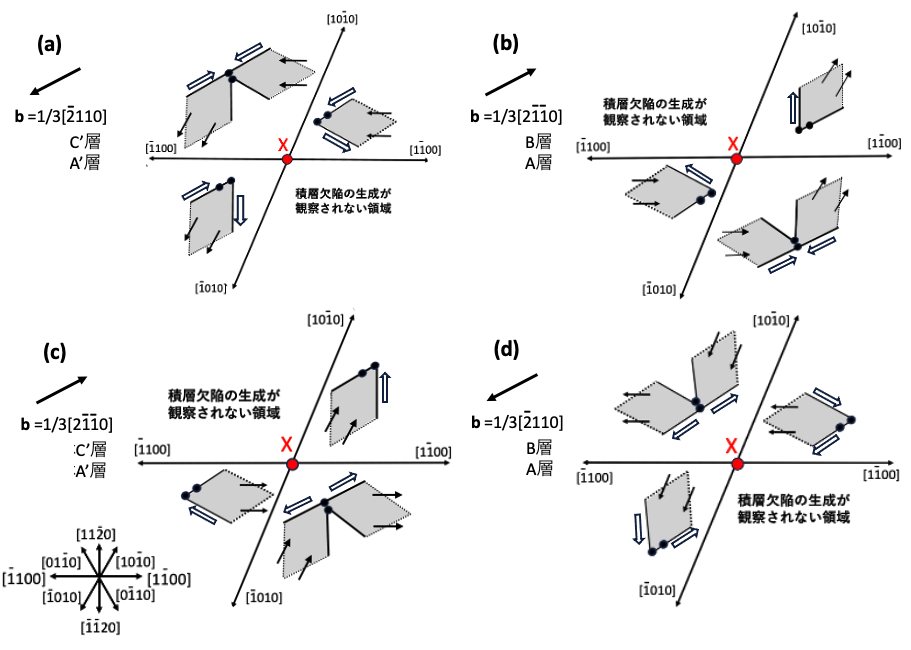
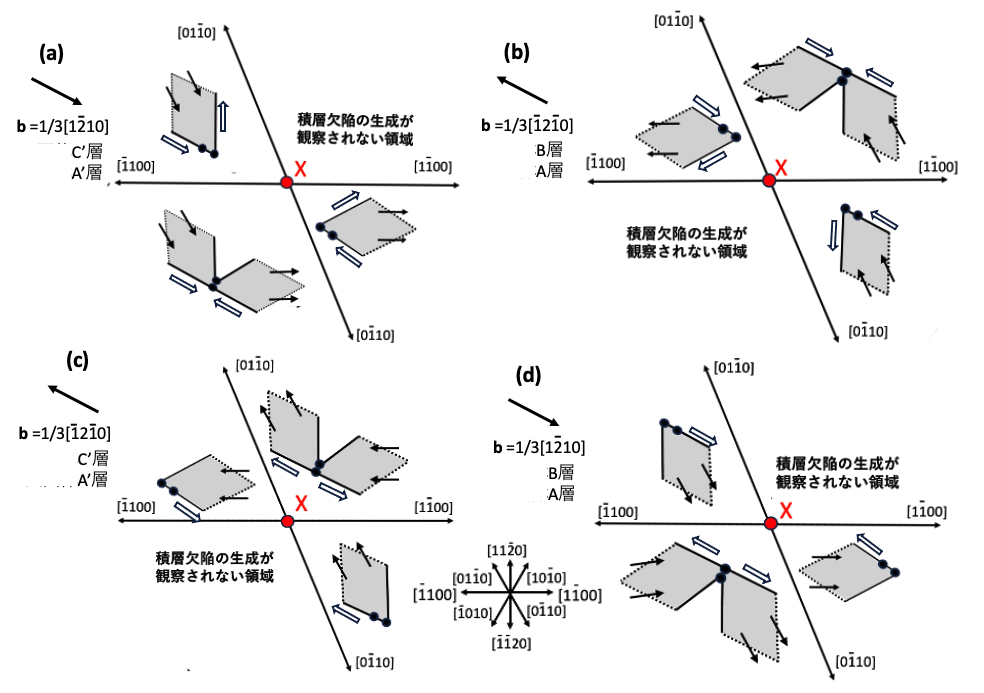
図9-5はb=1/3[1210]の基底面転位がn^–ドリフト層中で折れ曲がる場合を考察します。この場合、どのような形状の積層欠陥が生成するかは図5-8(b),(c)を参照すると容易に推察することができます。図9-5(a),(b)は折れ曲がった基底面転位の向きが11時方向から3時方向の場合です。図9-5(a)はこの基底面転位がA’層かC’層中に存在している場合です。六角形状積層欠陥の右縁のSiコア部分転位def部はこのまま右に移動して行き遮るものがなければMOSFET構造の右端まで積層欠陥は成長を続けます。図9-5(b)はこの基底面転位がA層かB層中に存在している場合です。六角形状積層欠陥の左縁のSiコア部分転位def部はこのまま左に移動して行き遮るものがなければMOSFET部の左端まで積層欠陥は成長を続けます。また、これらの図では、積層欠陥が成長しているフロント部分のdef部では、de部と,ef部の長さを同じ長さにして描いていますが、同じ長さではない場合もあると考えられます。

図9-5(c),(d)はb=1/3[1210]の基底面転位の折れ曲がり部分の向きが9時から11時の向きの場合です。この場合も図5-8(b),(c)から容易に推察されます。図9-5(c)はb=1/3[1210]の基底面転位がA’層かC’層中に存在する場合です。図9-5(d) はb=1/3[1210]の基底面転位がA層かB層中に存在する場合です。図9-5(a),(b)で現れている三角形状の積層欠陥が現れなくなります。図9-5(c)の積層欠陥もdefのSiコア部分転位部は遮るものがなければこのデバイスの右端まで成長を続けます。図9-5(d)の積層欠陥もdefのSiコア部分転位部は遮るものがなければこのデバイスの左端まで成長を続けます。

図9-5(e),(f)はb=1/3[1210]の基底面転位の向きが3時から5時方向の場合です。図9-5(a),(b)の図で現れている6角形状の積層欠陥は現れなくなり三角形状積層欠陥のみ現れますます。図9-5(e)は図9-4(a)の三角形状の積層欠陥と同様のものです。積層欠陥の縁の部分転位のバーガース・ベクトルや部分転位の向きも同じです。図9-5(f)は図9-4(d)の三角形状の積層欠陥と同様のものです。エピ層成長時のステップフローの向きは[1120]なので、貫通刃状転位の折れ曲がりの原因がステップフローと関連がある場合、3時から9時の間の方向へ貫通通刃状転位の折れ曲がり部分が向くことは、稀かもしれません。これらの積層欠陥はp層/n^–ドリフト層界面や、n^–ドリフト層界面/n⁺基板界面に到達すると成長が停止します。図9-5(e),(f)は成長が飽和して停止した状態です。

図5-8(b),(c)から容易に推察されるように、b=1/3[1210]の基底面転位の折れ曲がり部分の向きが5時から9時の方向の場合は積層欠陥の成長はありません。

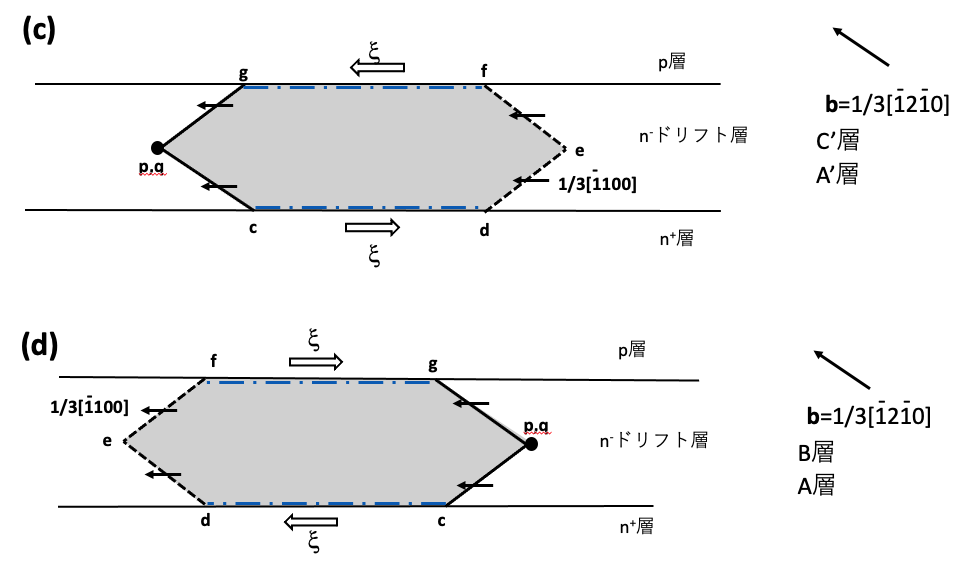
次に、b=1/3[1210]の貫通刃状転位がn^–ドリフト層中で折れ曲がる場合を考察します。この場合も、図5-8(a),(d)から容易に推察されます。折れ曲がり部分のb=1/3[1210]の基底面転位の向きが11時から3時の向きの場合は積層欠陥の成長はありません。b=1/3[1210]の基底面転位の向きが9時から11時の向きの場合を考察します。b=1/3[1210]の基底面転位がA’層、C’層中にある場合は、図5-8(a)から推察されるように図9-5(e)と同様の形状と構造の積層欠陥が現れます。b=1/3[1210]の基底面転位がA層、B層中にある場合は、図5-8(d)から容易に推察されるように図9-5(f)と同様の形状と構造の積層欠陥が現れます。ただし転位の向きは逆向きに設定していて、バーガース・ベクトルの向きも逆向きに設定します。

同様に、b=1/3[1210]の基底面転位の折れ曲がり方向が5時方向から9時方向までの場合は図9-5(a),(b)と同様の形状の積層欠陥が現れます。また、同じように、b=1/3[1210]の基底面転位の折れ曲がり方向が3時方向から5時方向までの場合は図9-5(c),(d)と同じような形状の積層欠陥が現れます。これらは、図5-8を参照すると容易に推察することができると思います。b=1/3[1210]の貫通刃状転位の折れ曲がりでも説明しましたが、貫通刃状転位の折れ曲がりの基底面転位部分が、3時方向から6時を経由して9時の方向の範囲に向くことは稀かもしれません。

ページ : 1 2 3