はじめに
前回までに、4H-SiC-MOSFETのn–ドリフト層部分にどのような転位組織が存在しているかを考察しました。REDG効果によって、これらの転位組織からどのような形状の積層欠陥が生成するのかを、連載(8)(9)(10)(11)で考察します。エピ層成長が始まると、基底面転位→貫通刃状転位への変換が発生しますが、n–ドリフト層のエピ成長が始まって、変換が発生するまでの短い基底面転位部分からREDG効果により成長する積層欠陥の形状についてこの連載(8)で考察します。
(A) 基板中のb=±1/3[1120]の基底面転位のn–ドリフト層部への侵入に起因する積層欠陥の形状
この考察では、n+層の基板の上にn–ドリフト層をエピ層成長によって形成することを想定しています。基板中の基底面転位は、エピ層成長によって貫通刃状転位へ変換されますが、エピ層成長が始まるとすぐにこの変換が発生するわけではないことはすでに説明しました。基板中では、基底面完全転位は2つの基底面部分転位に分解していて、2つの部分転位の間には幅の狭いショックレー型積層欠陥が存在しています。貫通刃状転位への変換が起こる前に、まず2つの部分転位が接近して合体し1本の基底面完全転位に戻り、その後貫通刃状転位への変換が起こります。
基底面転位をTEMで観察すると、2つの基底面部分転位の間に存在するショックレー型積層欠陥の幅に多少のバラツキがあることがわかります。エピ層成長が開始されると2本の基底面部分転位が合体して1本の基底面完全転位が形成され、貫通刃状転位に変換されます。積層欠陥の幅にバラツキがあると、貫通刃状転位に変換されるまで、エピ層中での基底面転位の長さは異なっています。拡張幅が狭い場合、エピ層成長が始まるとすぐに貫通刃状転位へ変換されますが、拡張幅が広いと、ある程度エピ層成長が進行しないと貫通刃状転位へ変換されないと考えられます。TEMによる観察では数10ナノメートル程度の長さの基底面転位がn–ドリフト層中に入り込んでいることが報告されています。
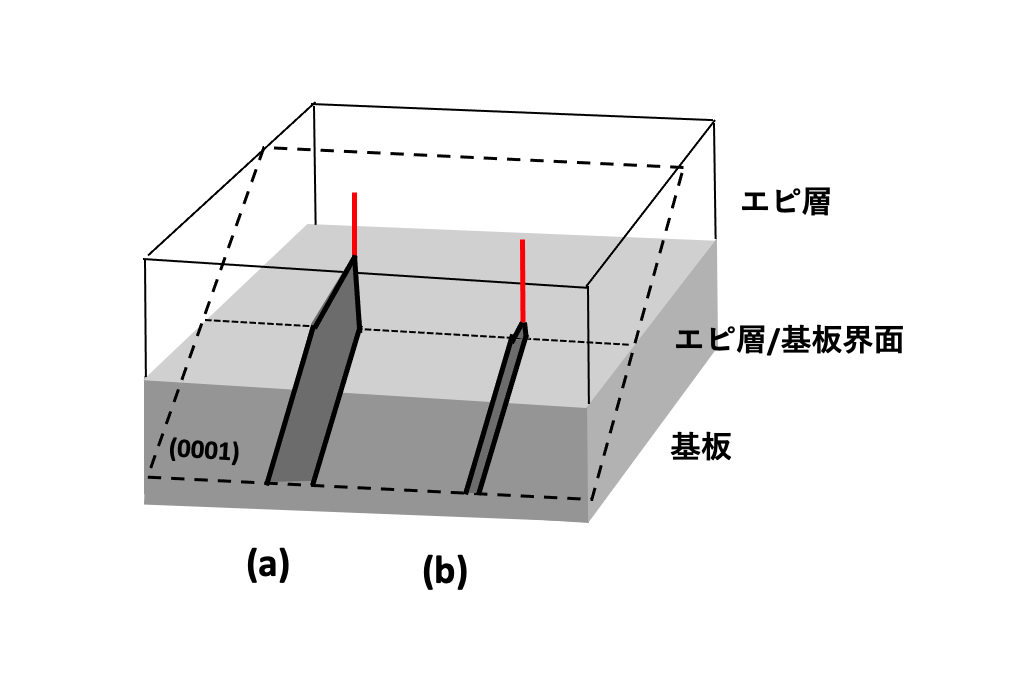
つまり、基板中から引き継がれた基底面転位がn–ドリフト層中(エピ層中)にある程度の長さで入り込んでその後変換され、そして入り込む長さにはバラツキがあると考えられています。図8-1は、この状況を模式的に示しています。基底面転位の拡張幅(ショックレー型積層欠陥の幅)のバラツキや、基底面転位の向きのバラツキがあり、変換に関してある程度のランダムな状態であることが推察されます。
次に、n–ドリフト層中に入り込んだ短い基底面転位はREDG効果によってどのような形状のショックレー型積層欠陥を生成するのかを考察します。
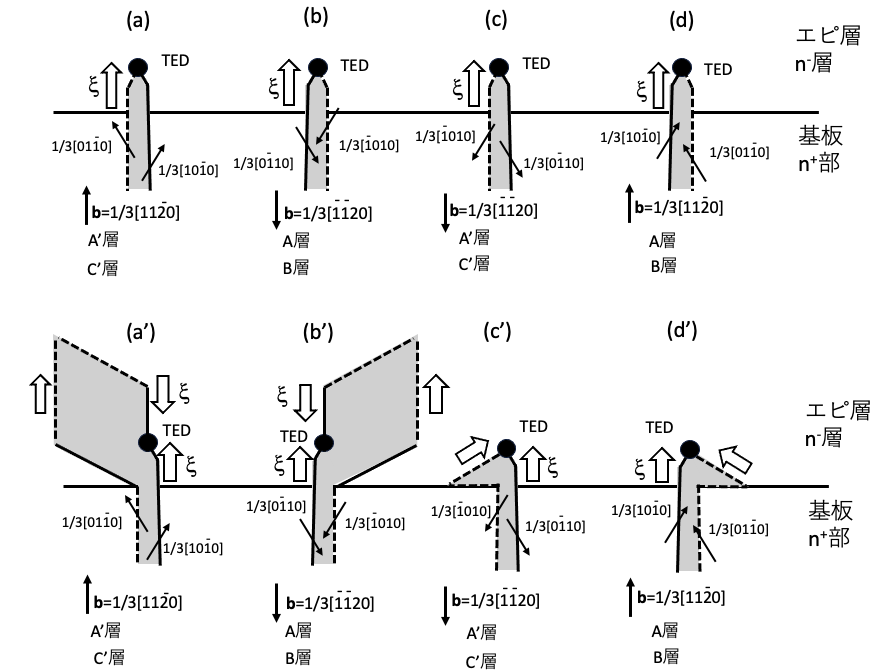
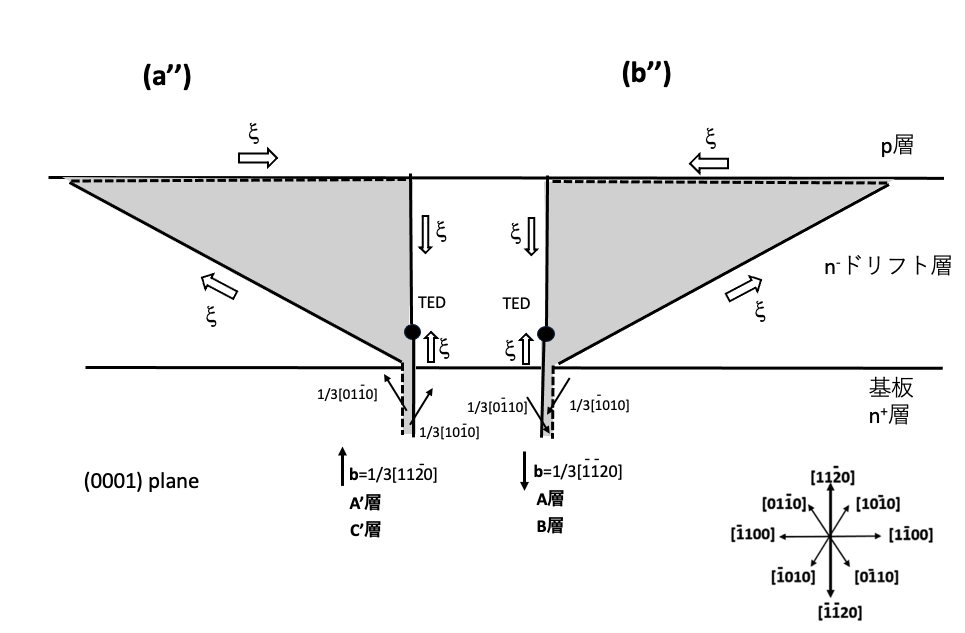
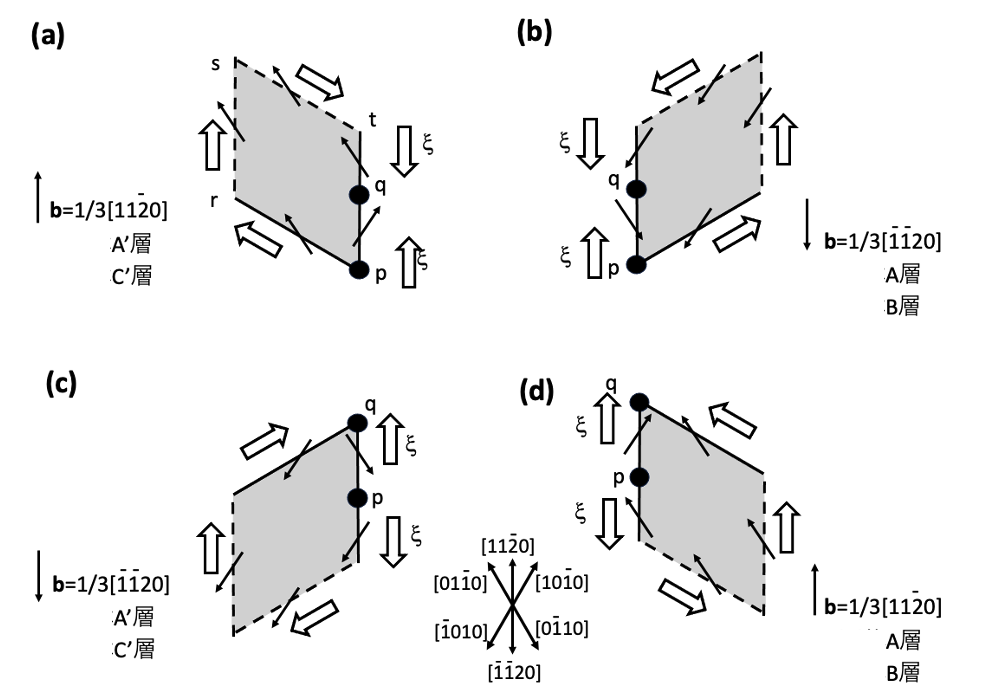
図8-2(a),(b),(c),(d) は基板中に存在していたb=±1/3[1120]の基底面転位が、少しだけn–ドリフト層(エピ層)中に入り込んで貫通刃状転位へ変換された状態を示しています。これらの図は[0001]方向から見た状態を示しています。(a’),(b’),(c’),(d’)はREDG効果により(a),(b),(c),(d)から積層欠陥が成長している状態を模式的に示しています。REDG効果は主にn–ドリフト層中で発生しn+部では発生しないと想定します。つまり積層欠陥はn–ドリフト層中で成長し、エピ層/基板界面で成長停止します。図8-2 (a),(b),(c),(d)は、連載その(4)図4-2 (a),(b),(c),(d)と同じ構造です。REDG効果により図4-2 (a),(b),(c),(d)から図4-3(a),(b),(c),(d)に示すように積層欠陥が成長します。またこれは図5-6(a),(b),(c),(d)の各図の11時から1時の場合の積層欠陥の成長状態です。これらの図を参考にして、n+部分での積層欠陥の成長が抑えられた図を描くと図8-2(a’),(b’),(c’),(d’)になります。図8-2 (c’),(d’)に示す小さな三角形の積層欠陥はこのまま成長停止状態になります。図8-2(a’),(b’)に示す菱形の積層欠陥はこのまま成長を続け、p層中では成長しないことを想定し、この菱形の上部はp/n–ドリフト層界面に到達すると成長停止し、図8-2(a’’),(b’’)に示す正三角形の半分の直角三角形の形状の積層欠陥になります。図8-2(a’’),(b’’)は積層欠陥の成長が飽和した状態です。図8-2(a’),(b’),(c’),(d’)のから理解できることは、同じバーガース・ベクトルを持っているb=±1/3[1120]の基底面転位でも、どの四面体層のすべり面に基底面転位がのっているかに依存して、積層欠陥がほとんど成長しない場合があることです。単純に考えると半数のb=±1/3[1120]の基底面転位からは積層欠陥はほとんど成長しないと考えられます。
図8-2(a),(b),(c),(d)では全ての転位の向きは[1120]方向に向けて描いています。エピ層成長が始まると基底面転位はなるべく短くなるように[1120]方向に向きを変えていくと推察されるので、転位の向きを[1120]方向に設定しています。この方向からずれていたとしても、図5-6(a),(b),(c),(d)を見ると、それぞれ基底面転位の向きが11時の方向から1時の方向であれば、図8-2(a’),(b’),(c’),(d’)のように積層欠陥は成長することが推察されます。
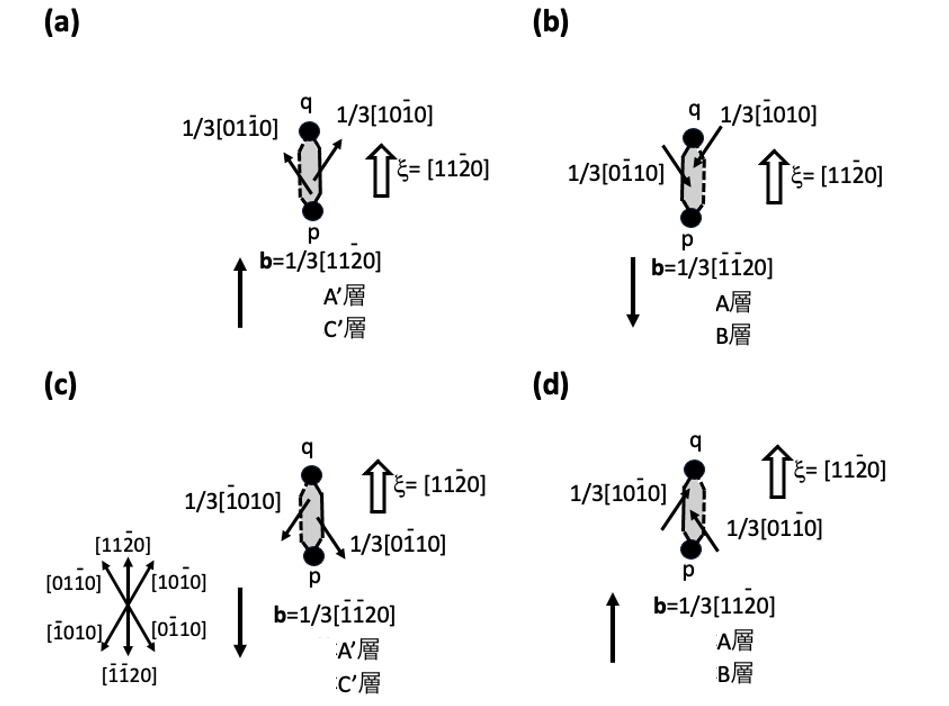
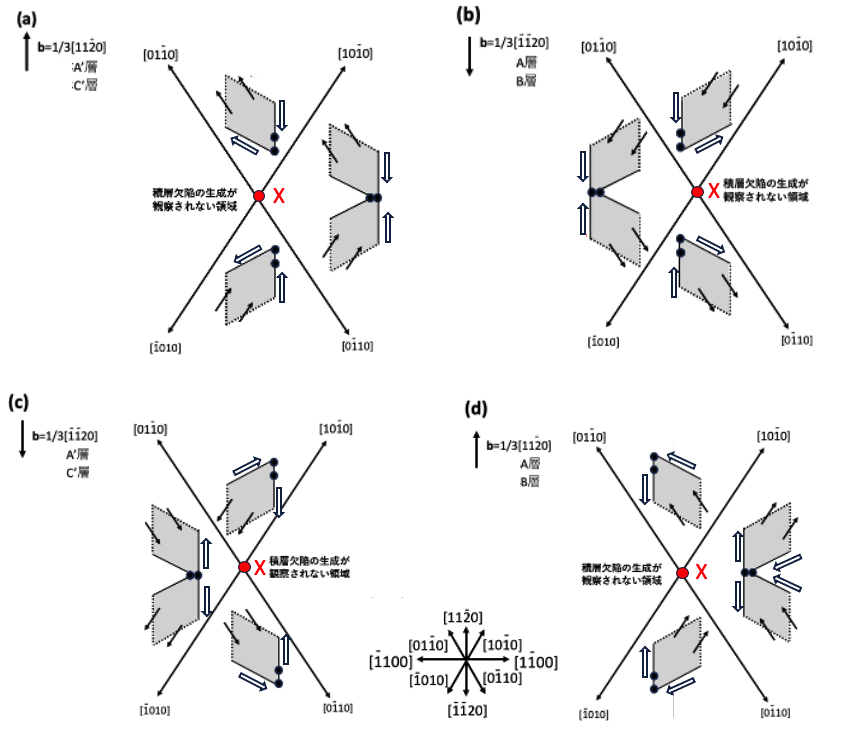
b=±1/3[1120]の基底面転位が11時の方向から1時の方向の範囲以外の他の方向を向いている場合を考えます。b=1/3[1120]の基底面転位がA’層かC’層のすべり面にのっていている場合を例として考えます。この状態での基底面転位の向きと成長する積層欠陥の関係は図5-6(a)に示しています。基板中に存在していた基底面転位がエピ層中に引き継がれるためには、基底面転位の向きは図5-6の各図の9時から12時の方向を過ぎて3時の向きを考慮すれば十分なので、ここではそれ以外の向きは考慮する必要はないと考えられます。b=1/3[1120]の基底面転位の向きが9時から11時までの間の向きでは積層欠陥は成長しません。同じバーガース・ベクトルを持っていても積層欠陥が成長しないのです。
図5-6(a)の図で1時から3時方向の範囲の基底面転位の向きでは2重菱形の積層欠陥が現れることになっていますが、2重菱形の積層欠陥のうち下側の菱形積層欠陥はn+層に入り込んでしまうので、この下側の菱形積層欠陥は大きくは成長せず、上側の菱形積層欠陥が大きく成長します。つまり、図5-6(a)の11時から1時の方向の範囲に基底面転位が向いている時に現れる積層欠陥と同じような積層欠陥が現れます。これは図8-2(a’),(a’’)と同様の形状の積層欠陥です。
b=1/3[1120]の基底面転位がA層かB層中のすべり面にのっている場合の積層欠陥の成長の状態は、図5-6(b)に示されています。b=1/3[1120]の基底面転位の向きが11時から1時の範囲の場合は図8-2(b’)の形状の積層欠陥がREDG効果によって現れますが、9時から11時の向きの範囲では2重菱形積層欠陥が現れることを図5-6(b)は示していますが、結局、下側の菱形積層欠陥の成長は停止するので図8-2(b’)の場合とほぼ同様の形状の積層欠陥が現れます。そして、b=1/3[1120]の基底面転位の向きが1時方向から3時方向の場合は積層欠陥の成長はありません。積層欠陥が成長しない条件が現れます。
b=1/3[1120]の基底面転位がA’層かC’層中のすべり面にのっている場合を考察します。この場合は、図5-6(c)に示されています。基底面転位の向きが11時方向から1時方向の範囲だと結局、図8-2(c’)の状態なので積層欠陥の成長はほとんど無いと考えられますが、b=1/3[1120]の基底面転位が9時から11時の方向を向いていると図5-6(c)に示されているように2重菱形積層欠陥が成長することになっています。しかしなが、2重菱形積層欠陥の下側の菱形積層欠陥はn+層に入ってしまうので成長停止し、上側の菱形積層欠陥のみが成長します。そして、図8-2(a’)(a’’)に示す形状と似た形状の積層欠陥が現れますが、図8-2(a’)(a’’)に示す積層欠陥とは、部分転位の向きとバーガース・ベクトルの向きが逆になっています。このことはほぼ同一の積層欠陥であることを示しています。また、b=1/3[1120]の基底面転位が1時方向から3時方向の範囲を向いていると、積層欠陥の成長はありません。11時から3時までの方向の範囲では、結局、とても小さな積層欠陥の成長か、積層欠陥の成長はないと考えられます。
次にb=1/3[1120]の基底面転位がA層かB層中のすべり面に乗っている場合を考察します。これは、図5-6(d)の状態です。基底面転位の向きが9時から11時の方向の範囲では積層欠陥は成長せず、11時から1時までの範囲も、基板方向へ少し成長して成長停止状態になります。基底面転位の向きが1時から3時の方向の場合、図8-2(b’),(b’’)と似たような形状の積層欠陥が現れます。
以上の考察から、b=±1/3[1120]の基底面転位がエピ層中に入り込んでも、意外と積層欠陥が成長しない条件が色々と現れていることが理解されると思います。REDG効果後に顕微PL法などで観察すると、正三角形の半分の直角三角形が観察される場合、それは基底面転位から貫通刃状転位への変換部分のb=+1/3[1120]の転位が原因のショックレー型積層欠陥の可能性があります。(a’’)のような場合は、四面体A‘層またはC’層中のb=1/3[1120]の基底面転位、(b’’)のような場合は、四面体A層またはB層中のb=1/3[1120]の基底面転位が貫通刃状転位への変換の際にn–ドリフト層中に入りこむ事が原因だと考えられます。ただし、後に述べますが、これらの転位以外にも三角形状の積層欠陥を生成する転位や条件が存在するので注意が必要です。それらの詳細は後に示します。
次にb=1/3[1210]の基底面転位が、基底面転位→貫通刃状転位へ変換部分の基底面転位がREDG効果によりどのようになるのかを考察します。







コメントを残す