アイシーソルーションズ, LLP

b=1/3[1120]の基底面転位が色々な方向を向く場合を考察するためには、転位の向きがぐるりと360度回転する基底面転位ループを考察すれば良いのですが、この転位ループの構造は、下記の図2-3の図から簡単に描くことができます。図2-3はA’層中でξ=[1120]方向を向いたb=1/3[1120]の基底面完全転位が2つの部分転位と積層欠陥に分解している状態の図で、この図は単に図2-2の簡略版です。また、Siコア30度部分転位がどういう時に出現するかを知るには、円形の転位ループではなく六角形状の転位ループで考察すれば簡単で十分です。図2-3を基にしてA’層中でのb=1/3[1120]の六角形状の転位ループを描くと図2-4になります。

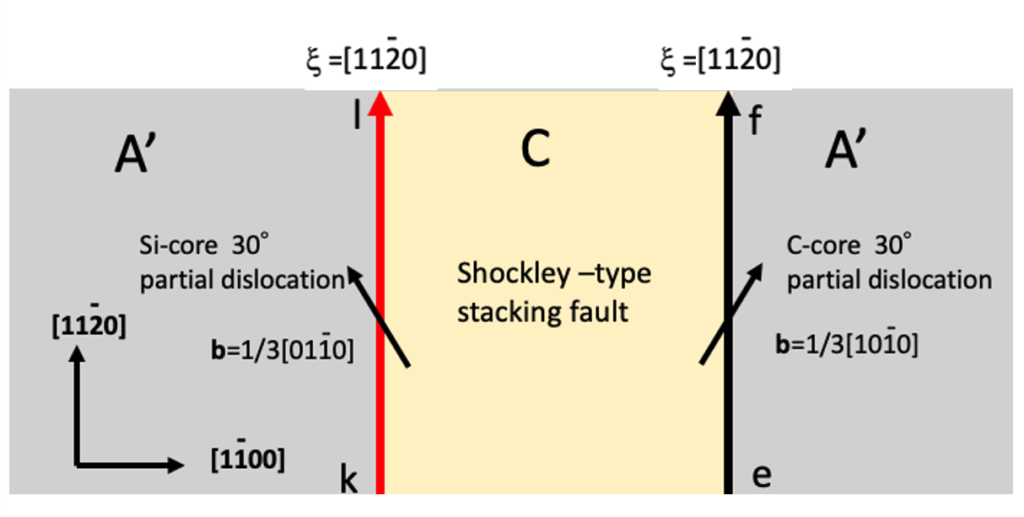
図2-4 では[0001]方向から見て転位ループの向きξは時計回り方向、白矢印方向に設定しておきます。Siコア30度部分転位部分klとCコア30度部分転位部分efは図2-3のkl部とef部の2つの部分転位と同じ転位です。図2-4は、この2つの部分転位で六角形の基底面転位ループを作成し、2つの部分転位の間に積層欠陥が形成された状態を示しています。ベージュ色の部分が積層欠陥です。それぞれの2つの部分転位の六角形ループに沿って2つのバーガース・ベクトルは保存されています。

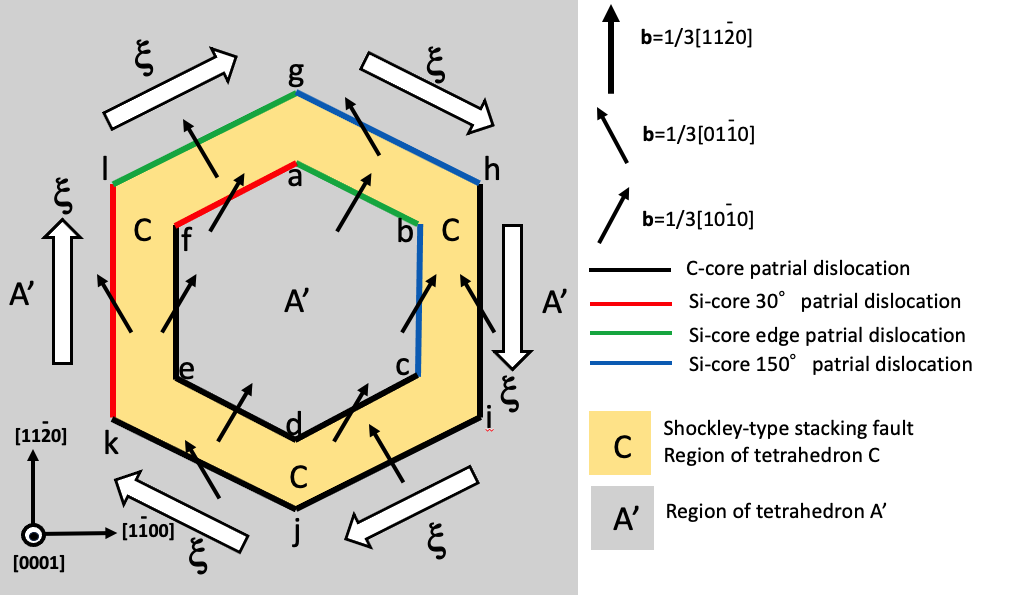
 2つの部分転位のバーガース・ベクトルは転位ループに沿って見ていくと、常に同じ方向を向いています。一方、部分転位の向きは、転位ループに沿って見ていくと、方向を変えながらぐるっと一回転します。部分転位の向きを基本にして転位に沿って見ていくと、バーガース・ベクトルは転位の向きの右側方向を向いたり、左側方向を向いたりします。[0001]方向から見て、転位の向きを基準にして転位の向きから右側にバーガース・ベクトルが向く場合はCコア部分転位です。Cコア部分転位を黒線で示しています。転位の向きよりバーガース・ベクトルが左側に成分を持つ場合はSiコア部分転位です。バーガース・ベクトルの向きと転位のコア構造の関係は、連載の前回の図1-7で説明しています。Siコア30度部分転位を赤線で示します。Siコア刃状部分転位を緑線で示します。Siコア150度部分転位を青線で示します。通常、Siコア30度部分転位がREDGを引き起こしますと色々な文献には記述されていますが、Siコア150度部分転位もREDGを引き起こします。REDGの実験結果を報告している文献では、観察される転位の向き自体を明確に設定していない場合もあり、とりあえずバーガース・ベクトルと転位との角度が30度のものは30度部分転位と報告しています。30度部分転位も150度部分転位も、転位の向きを明確に定義しなければ、バーガース・ベクトルと線状の転位とのなす角は30度です。しかしながら、後の連載(4)で詳しく述べますが、Siコア30度部分転位とSiコア150度部分転位とでは、成長する積層欠陥の形状の向きが異なります。

以上で、A’層中で発生するb=1/3[1120]の完全転位が、部分転位に分解した状態で、どの向きに向いた部分転位にSiコア30度部分転位やSiコア150度部分転位が発生するかは示すことはできたと思います。赤線部や青線部が危険な部分とこの図からは考えられます。ちなみに、重要なことに注目しておくと、この転位がξ= [1120]方向を向いているときは、積層欠陥の左側kl部はSiコア部分転位が位置していて、積層欠陥の右側のef部はCコア部分転位です。そして、この転位がξ= [1120]を向いているときも、積層欠陥の左側bc部はSiコア部分転位で、積層欠陥の右側のhi部はCコア部分転位です。後にこれらの事が意味を持っていることに気づきます。

さらに他のバーガース・ベクトルの基底面転位ループではどうなっているかを知りたいわけですが、そのことを考察するには、4H-SiCの結晶がどのような対称要素を持っているかを知る必要があります。4H-SiCの結晶の対称性について考えてみましょう。

4H-SiCの結晶の対称性

4H-SiC結晶は、空間群P6₃mc の構造とされています。国際結晶学連合の表にはP6₃mcはNo. 186の番号が割り当てられていています。ここではこの解説で必要となる対称要素のみ取り出して考察します。

(1120)面を適切に選ぶと、(1120)面は鏡映面になります。4H-SiC結晶ではこの面の片側と反対側は鏡映対称の構造を持っています。つまりこの(1120)面を中心に鏡映反転操作を行うと、この操作を行う前の結晶構造と同じ構造になります。鏡映反転操作を行う前の結晶構造と後の構造は区別がつかないということです。

(1100)面を適切に選ぶと、(1100)面はc映進面になります。c映進面(c-glide plane)とは、この面を用いて鏡映反転操作を行い、さらにc軸方向にc/2の長さだけ結晶全体を平行移動させると、これらの操作を行わない元の構造と同じ構造になる面です。c映進操作を行う前の構造とc映進操作を行った後の構造とは区別がつきません。

さらにこの結晶構造にはc軸方向に沿って3回回転軸があります。この軸を中心に120度反時計方向に回転すると、回転する前の構造と同じ構造が出現します。同様なことですが、この軸を中心に240度反時計方向に回転すると回転する前の構造と同じ構造が出現します。つまり、回転操作を行う前の構造と回転操作を行った後の構造とは区別がつきません。

これらの (1120)鏡映面、(1100)c映進面、3回回転軸の位置を単位胞中で図示すると、図2-5のようになります。

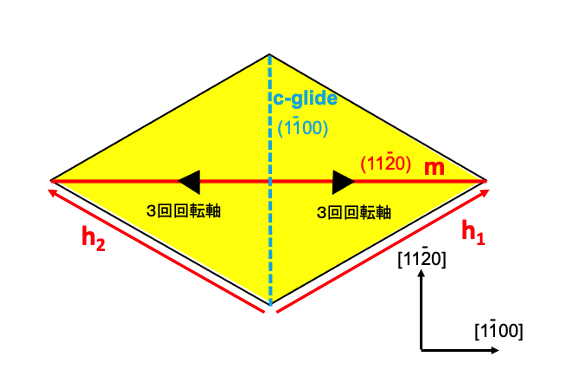
図2-5 はP6₃mcの対象要素のうち今回の話で利用する対象要素のみを示しています。その他の対称要素は利用しないので省略します。図2-5に示す対称要素を利用して他のバーガース・ベクトル、他の四面体層中での転位ループの構造を考察します。

ページ : 1 2 3 4