アイシーソルーションズ, LLP

　前回の第3回記事では、六方晶系と三方晶系の関係を整理し、HCPベースの六方晶結晶を対象に対称性の違いによる欠陥発生を考察した。それに引き続き今回は三方晶系の結晶と六方晶系の結晶の違い、並びに単斜晶系の特徴を特に積層構造の点から詳しく観た後、本連載のまとめを述べたい。

７．積層構造の結晶系

　前回記事の後半では、最密充填構造を持つ層を規則正しい層内シフトを伴って積層させることで出来上がる結晶構造と欠陥の整理を行い、その表記法としてのZhdanov表記を紹介した。c軸方向への積層構造に関して、重要なポイントは次の通りである。

• 層を形作る格子は六方ネットであり、原子を配置できるのは、格子点であるAサイト、面内座標が(2/3, 1/3)のBサイト、(1/3, 2/3)のCサイトの３サイトである。
• 層の構造として、層群p 3m1の対称性をもつα構造とそれを層に垂直な軸で180˚回転させたβ構造がある。（名称に関しては、この両者を区別するだけの意味で何でも良い。またどちらがαでもβでもよい。）
• ある層の直近上層の格子点サイトは直近下層の格子点サイトに対してα構造では”A→B→C→A→. . . .”、 β構造では”A→C→B→A→. . . .”というように、層構造によって一意的に決まる。この関係は、図4-1の三角プリズム図⁷⁾でうまく表現できるとされている。

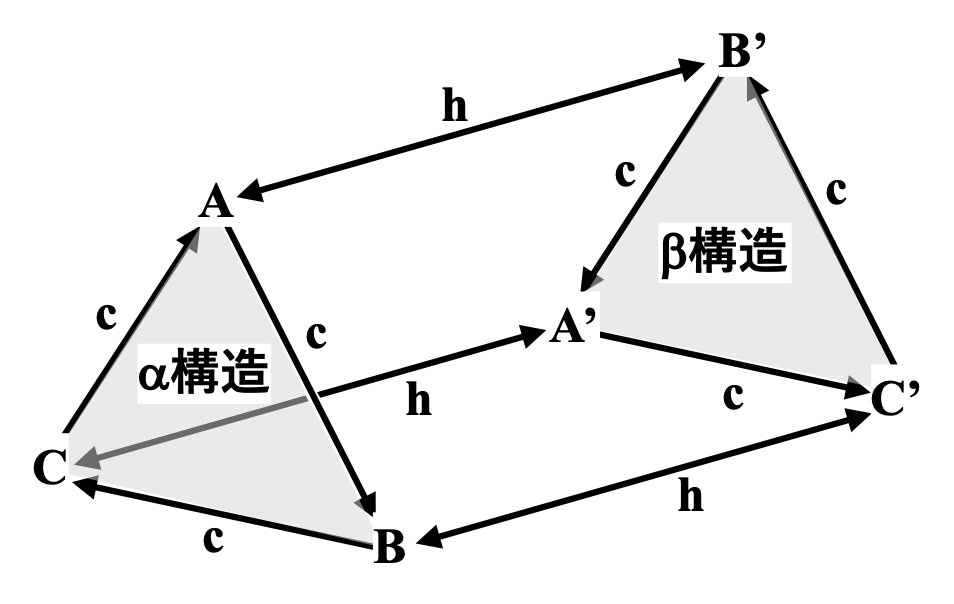
　Zhdanov表記を用いた積層構造に関して、理屈の上では(m₁ n₁ m₂ n₂ . . . . m_r n_r)で表される任意の構造が並進対称性をもつのは自明であり、その構造に対応する結晶を考えることが出来る。それではその結晶系はどうなるであろうか。

　第1層で格子点はAサイトにあるとする。その上に(m₁ n₁ m₂ n₂ . . . . m_r n_r)の積層構造を作ったとしよう。上記の重要ポイントより、各層の格子点はA, B, Cサイトのいずれかである。1周期内の層の層数をL=Σ（m_i+n_i）とした時、L+1層目の格子点サイトが１層目と同じAサイトの場合、１層目とL+1層目の間隔をc軸長とした単純六方格子をユニットセルとする結晶系、即ち六方晶系の結晶となる。例えばウルツ鉱型の積層構造は(1 1)で表されるが、このケースではL=2であり、確かにc軸長として２層分をとったHCP構造である。6H-SiCの場合は(3 3)でL=6となり、こちらも確かに6層周期の六方晶結晶である。

　では、L+1層目の格子点サイトがB或いはCサイトならどうであろうか。一見単純単斜格子風のものが出来る様にも思われるが、実は1層目からL層目までの構造を３回繰り返すことで、図3-4に示したような菱面体格子が出来上がる。この一例を挙げれば15R-SiCの結晶（Zhdanov表記で(3 2)₃=(3 2 3 2 3 2 )、L=15）がそれに相当する。表記としての基本周期である(3 2 )の次の層では、格子点がBサイトになり、2周期目でCサイト、3周期目でAサイトに戻ってきている。サイトと層構造の対応としては、”ABCA’C’BCAB’A’CABC’B’A”となる。図4-2に15R-SiCの積層構造を示すが、この表記に合致していることと16層目が１層目と同じサイト配置であることを読者の皆さんも確認してほしい。そして、3周期を考えれば図4-2の赤実線で示すような単純三方格子を設定することができる。但し、c軸方向の極めて長い周期が影響して、長い基本並進ベクトルと小さい並進ベクトル間角度が特徴的な大きく引き延ばされた三方格子となる。当初の問いへの答えとしては、「基本周期構造の終点サイトが同じであれば六方晶、異なれば三方晶である。」となる。

　先に、「理屈の上では任意の積層構造が可能」と述べたが、実際SiCの結晶としては200種以上の結晶多型が実際に見出されおり、その全てが六方晶か三方晶（3Cを含む）である。しかし、ある特定のポリタイプを純粋に作成しようとしても、(0001)面上の成長に限って言えば大抵の場合うまく行かない。今まで述べてきたように、α構造とβ構造の間の層構造転換がある意味偶発的に起こるからで、長い周期性が維持される、或いは遠く離れた層の構造が正確に最表面に伝搬する（15Rの例で言えば15層離れた部分の構造情報）、といったことが確率的にほとんどあり得ないからである。特に8層周期以上の周期性がマクロスケールで自然に生まれることはほとんどないと言って良いであろう。理屈の上では9R（Zhdanov表記で(2 1)₃或いは(4 5)）と言うような多型も可能ではあるが今までにそのような存在は確認されていない。現実に観測されている15Rの結晶多型も4Hや6Hの結晶中に部分的に混入したもので、母体の結晶多形からするとある種の”欠陥”でしかない。

　4Hや6Hの人為的な作成では、β構造の発生をうまく制御してマクロスケールの結晶が実現する何らかのドライビングフォースが働く条件を利用しているはずである。その手法の一つが微傾斜基板の原子レベルのステップを利用する”ステップ制御エピタキシー”⁸⁾である。通常のエピタキシャル成長では、上層の形成中に下地の構造情報が伝わることで同じ結晶構造が出来上がるが、再表面での原料種の拡散長が十分な場合には、図4-3のように原料種はステップ端まで拡散してそこで結晶に取り込まれ、ステップが伸張する。これは、エピタキシーが下地のみならずステップ端を介して横方向の構造情報も引き継いでいることを意味し、そのことによって全体としての層構造が維持されていると考えられる。

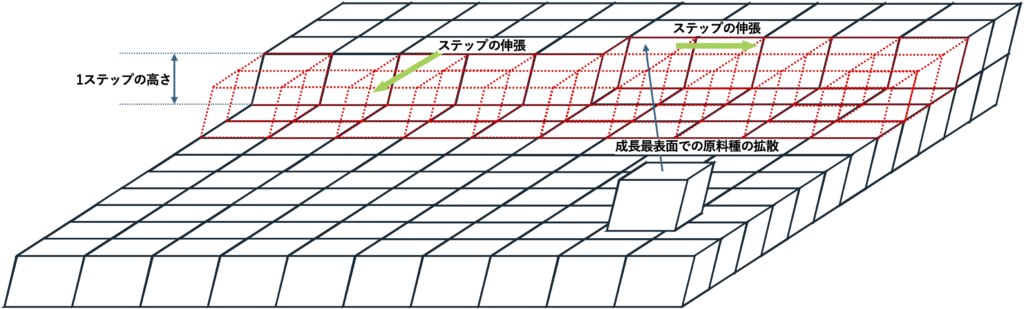
 　このステップ制御エピタキシーでは、オフ角と呼ばれる微傾斜の角度（〜数度）、方位とステップの横方向への進展、即ち層状成長を実現する条件が極めて重要となっている。SiCのエピタキシャル成長で他ポリタイプの混入がない高品質なエピタキシャル成長膜を得るためには、数度オーダーのオフ角が必要とされている。III-V族化合物半導体のエピタキシャル成長においても、通常使われている(001)面ジャスト基板と呼ばれる面でも実は0.1度オーダーのオフ角が存在しているようである。しかしながら、積層の周期が極端に長くなれば当然のことながらマクロなスケールで適用するのが困難となる。むしろ(0001)とは異なる別指数の面上への成長と捉えるのが妥当であろうか。図4-2の15Rで言えば、周期性が表れやすい緑の実線で示す(1 1 0 5)面などがあり得るかもしれない。但し、その際には層構造がp 3m1ではなくなり、縦横比が大きく異なって対称性が低い長方形ネット的なものになるであろうし、そもそも層状成長の前提である原子レベル平坦性が悪化してしまう。その積層の制御は(0001）面に比べればかなり困難であろう。

ページ : 1 2 3 4