アイシーソルーションズ, LLP

２．結晶成長と結晶の対称性

　さて、実際に起きる結晶成長の過程において結晶の対称性はどのように維持されるであろうか。結晶成長の意味を改めて考え直してみよう。結晶原料であるミクロな原子集団からマクロスケールの固体結晶への成長が起こるには、まず最初に”点”である原子集団が何らかの意味で合体していくことが必要である。いわゆる“種なし成長”では最初に自然核形成が起こるが、それは自由空間において原子集団が方向性を持たずに合体したものと考えても良い。しかし非晶質でない限り、自然形成核と言えどもミクロな範囲では結晶を成り立たせる対称性は保たれているであろう。そして結晶性を持った自然形成核がある程度のサイズを持てば、その後の成長はある結晶面上への成長と捉えても問題はないであろう（頂点や辺への成長というのは極めて考えにくい）。その意味で、この先の議論では“種あり成長”の土台としての基板結晶を想定し、その表面として現れている特定の結晶面上への結晶成長を対象とする。

　２次元面上への結晶成長で、下地基板の結晶情報がその上の成長層に引き継がれる薄膜成長現象をエピタキシャル成長と言うが、そのミクロレベルでの様式には次の３種が知られている。

1. 島状成長（Volmer-Weber型）
2. 層状成長（Frank-von der Merwe型）
3. 複合成長（Stranski-Krastanov型）

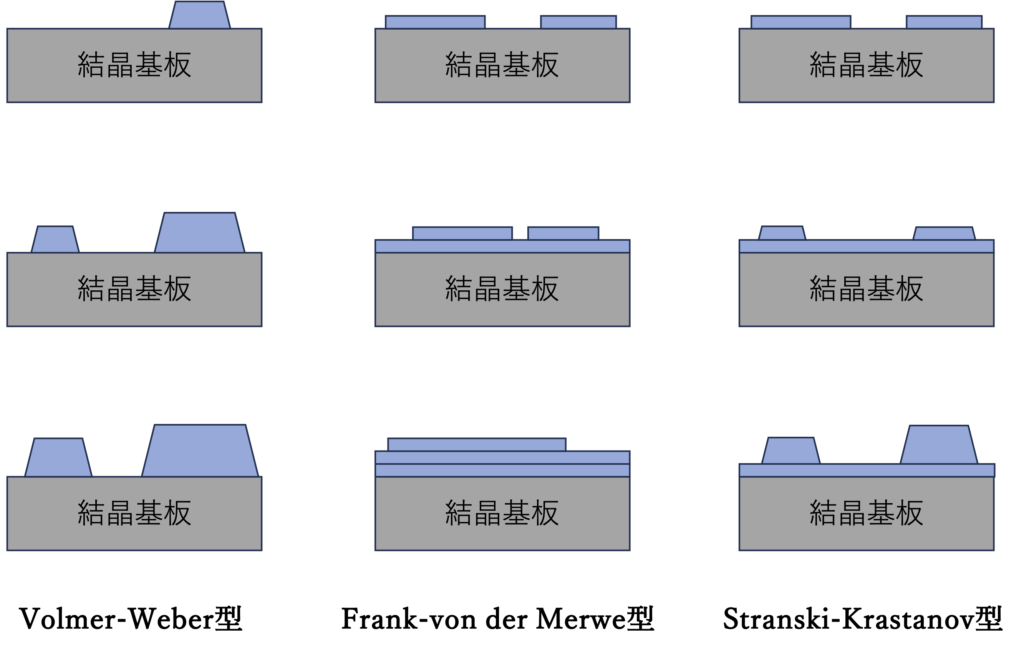
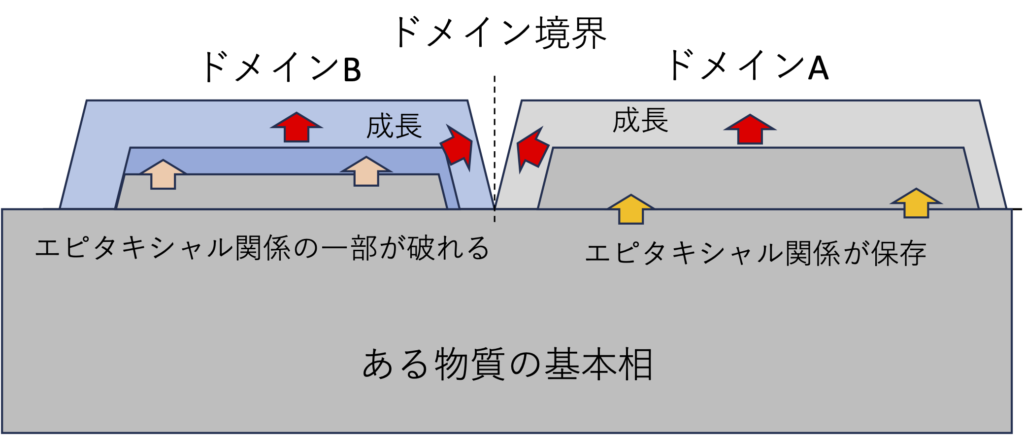
　これらのイメージを図1-4に示すが、理想的なエピタキシャル成長を行うためには(2)の層状成長が必須とされている。そしてその層が逐次重なって積層することで結晶ができあがる。しかし、ウェハーレベルのマクロなスケールに渡って完全に(2)の層状成長が実現することは極めて困難であろう。仮に、図1-4に示されるような完全にフラットな結晶基板面を用意出来ても、その上のある領域ではドメインAが、別の領域ではドメインBが別個に発生し、ドメイン内で層状成長が実現してもマクロなスケールではどうしても島状のドメインとなる。元の結晶基板も原子層レベルではフラットではあり得ず、原子層スケールの段差（ステップ）が生じていることもある。成長した両ドメインは、下地基板の上のエピタキシャル成長層として物質的、構造的には本来同じものである。成長が進むとこの両ドメインがあるところで衝突する。図1-5はこの様子を模式的に示したものであるが、島状領域発生の起点がドメインAとドメインBでは異なっていることから、この過程でドメインAとドメインBにはエピタキシャル関係のような直接的な構造伝搬は存在しない。理想的なケースとして、下地の構造情報が正しくAとBに伝搬していれば、AとBが衝突してもその間で結晶の並進対称性が維持され、合体したものは１つの結晶として成立する。しかしながら両者が衝突する前の層状成長の過程で、片方だけに何らかの結晶成長上の”間違い”が生じると、ドメインAとドメインBの対称性が同じである保証はなく、合体境界のところで結晶の並進対称性が崩れる状況が起こりうる。また、基板の歪み等により、両ドメインの結晶軸が微妙にずれることもあり得る。このような時、合体境界は結晶欠陥として認識されるものとなる。

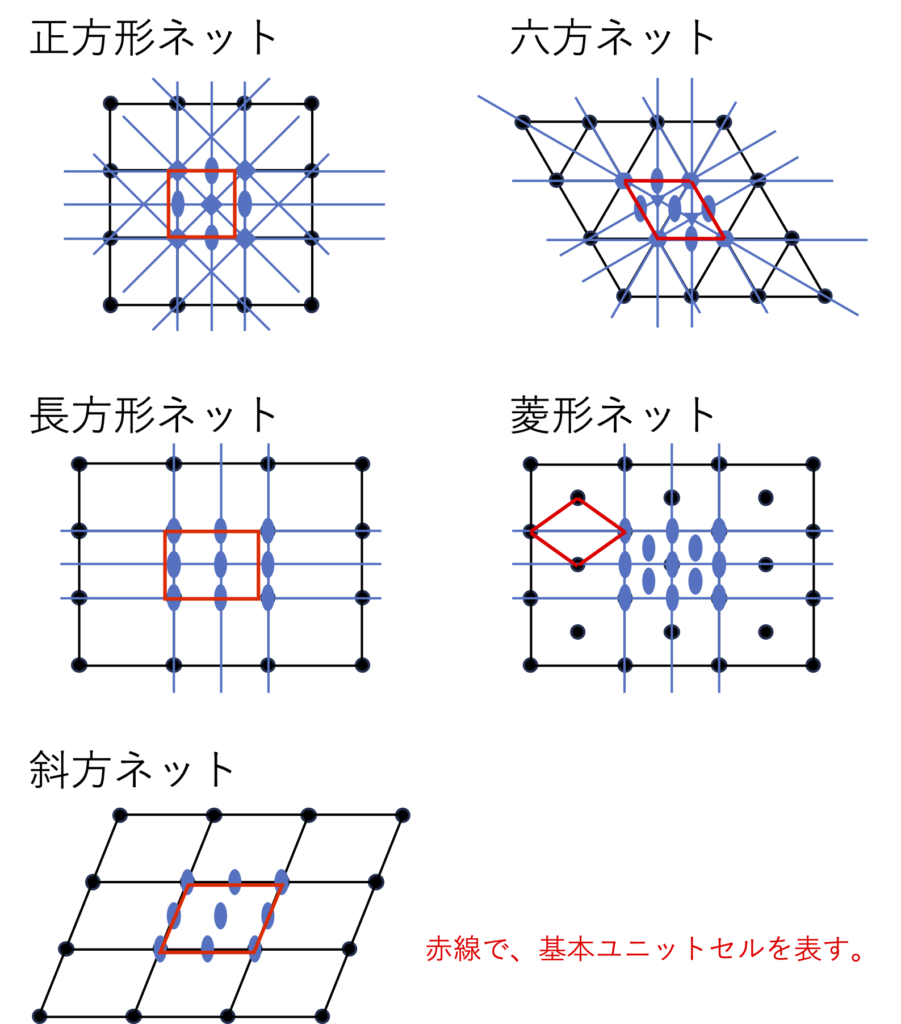
　エピタキシャル層状成長においては、積層する層に伝搬される構造情報は基本的には下地基板の表面層のものであり、この層としての対称性を始めとする構造情報が、積層する際に順次伝搬されることで３次元的な結晶が形作られる。層の対称性とは、わかりやすく言えば”平行移動で重なる壁紙“の対称性と同じものであり、２次元平面群（正確には、裏表が存在する“layer group”としてInt. Tables for Crystallography, Volume E^3）に掲載されている：日本語に訳せば「層群」であろうか）としてまとめられている。層群の情報が積層することで空間群に生まれ変わると解釈できる。層群は積層方向の情報を持っておらず、積層に際して本来の結晶として持つ空間群とは相容れない形になることが、先に述べた結晶成長上の”間違い”の正体と考えることができる。３次元の結晶構造と同様、２次元の層構造は格子＋基本要素と表現できる。そこでこの先の議論で頻繁に使う事になる2次元平面の２次元ネット（格子）を図1-6に示す。これらは３次元空間でのBravais格子に相当するものであり、図のように5種類に分類されている。

　連載本記事の初回として、半導体材料のエピタキシャル成長時の問題意識を結晶対称性の観点から紹介した。次回からは、実際の半導体結晶成長に則した実例を紹介しながら、各半導体材料の結晶構造上の特徴や共通点、差違、更には結晶構造や成長時の層の対称性がエピタキシャル成長に与える影響等について比較していきたい。

参考文献

1. “物質の対称性と群論”: 今野豊彦（共立出版, 2001）
2. “Int. Tables for Crystallography, Volume A, 6th edition”: Eds. M.I. Aroyo (Wiley, 2016)、 On-line版はhttps://it.iucr.org/services/purchase/
3. “Int. Tables for Crystallography, Volume E, 2nd edition”: Eds. V. Kopsky and D.B. Litvin (Wiley, Dec. 2010)

（続く）

ページ : 1 2 3